Куда течет ток - на примере трехфазной системы

Продолжаем изучение трехфазной системы электроснабжения. Вопрос, который мы будем рассматривать сейчас - куда течет ток. Несмотря на то, что данный вопрос не сложный, правильный ответ на него знают не многие. Даже некоторые электрики могут запутаться в путях протекания тока. Поэтому постараемся предельно доступно и наглядно объяснить особенности протекания тока в трехфазной системе.
Трехфазная система - пример схемы
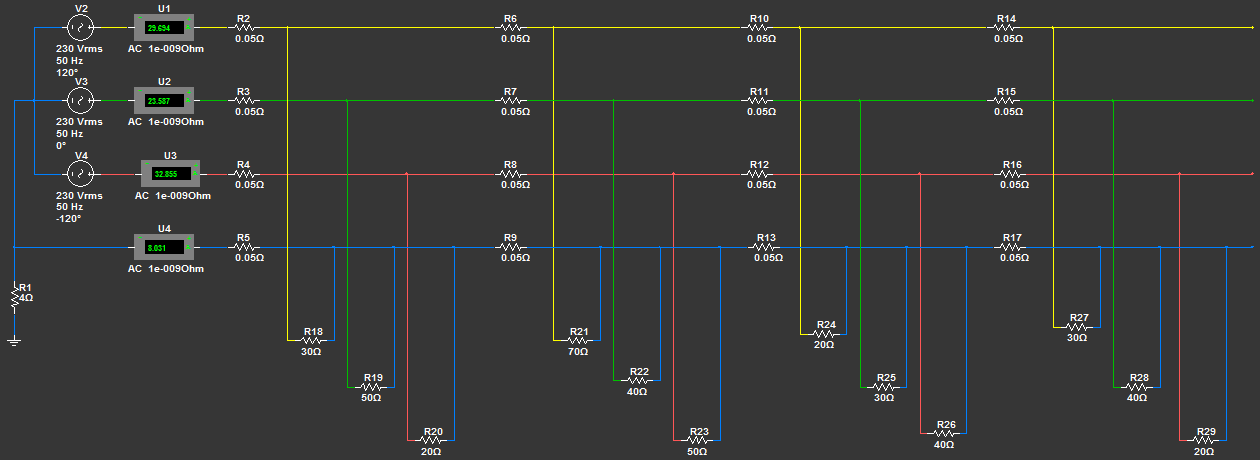
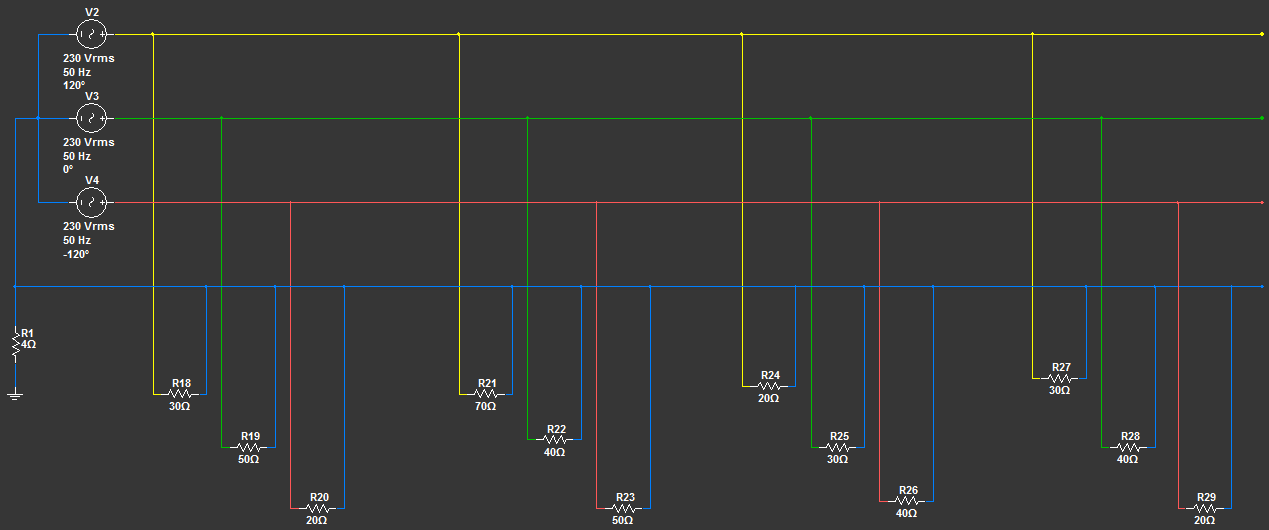
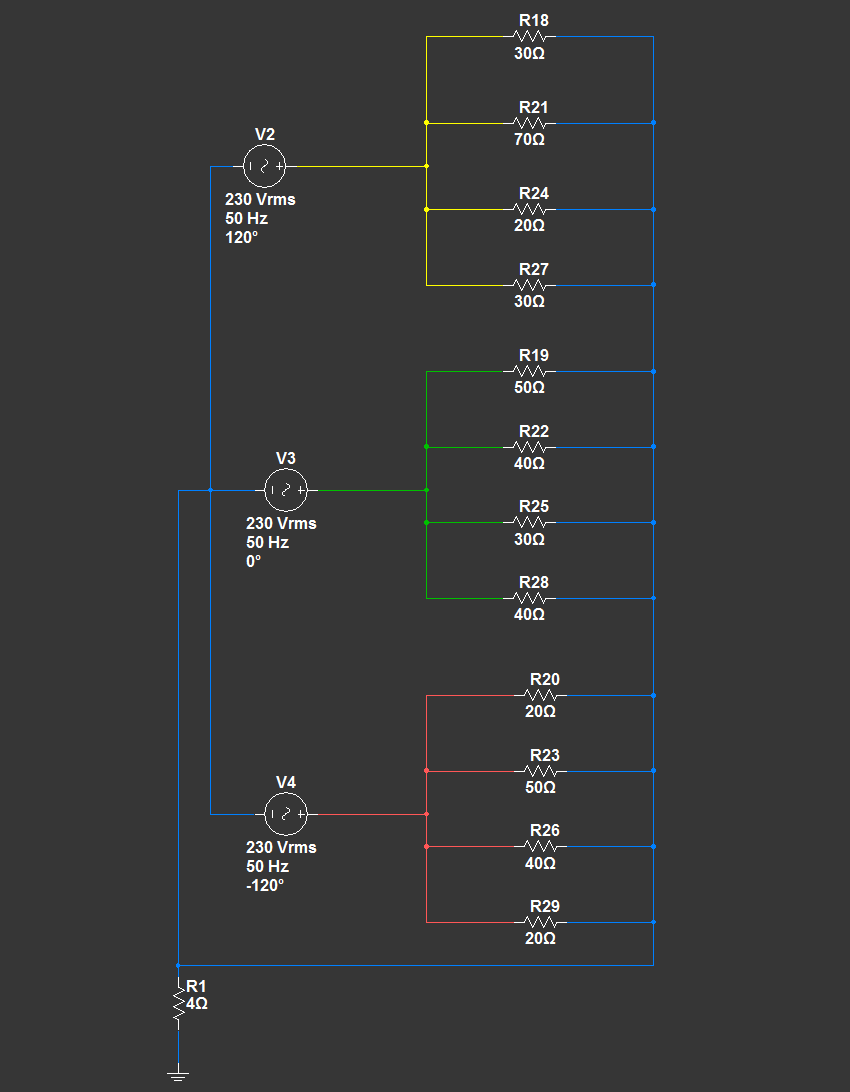
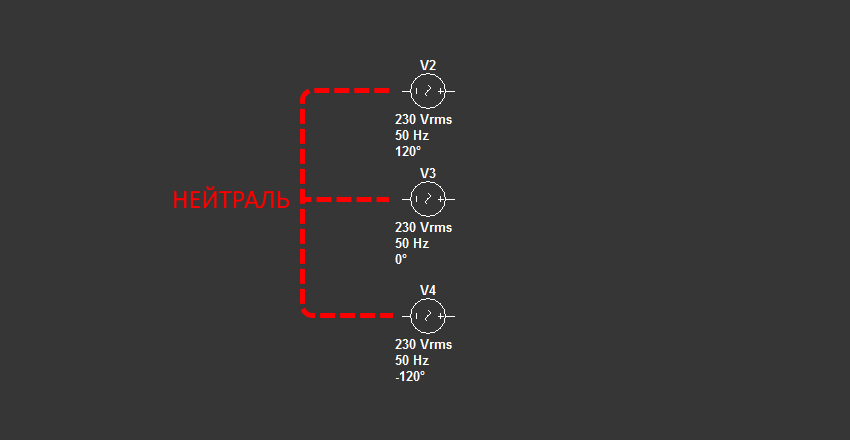
Ранее мы уже отрисовывали схему трехфазной системы в программе Multisim. Повторяться не будем как мы к ней пришли, приведем лишь схему:
Отметим каждый элемент схемы:
- V2, V3, V4 - три однофазных генератора переменного тока, соединенные вместе звездой и имеющие смещение обмоток друг относительно друга на 120°. Такая комбинация заменяет трехфазный генератор или трансформатор. В данном случае при помощи данных компонентов мы внесли в схему распределительный трансформатор, от которого по улицам электроэнергия передается конечным потребителям.
- R1 - сопротивление заземлителя нейтрали трансформатора (глухозаземленная нейтраль).
- R2 - R17 - сопротивление проводов на опорах.
- R18 - R29 - сопротивление конечных потребителей (домов, в которых включены в сеть электроприборы).
Особенность переменного течения тока в трехфазной системе
Прежде чем показывать путь течения тока в трехфазной системе важно разобраться с тем, что из себя представляет этот ток:
- Во-первых, ток у нас переменный.
- Во-вторых, ток - это упорядоченное движение заряженных частиц (в нашем случае электронов).
- В-третьих, так как ток переменный, то и упорядоченное движение электронов будет переменным в разные моменты времени.
- В-четвертых, скорость движения электронов не нужно путать со скоростью распространения электрического поля (близкой к скорости света). Средняя скорость упорядоченного движения электронов - это доли миллиметра в секунду.
- В-пятых, частота переменного тока 50 Гц. А это значит, что за секунду электроны 50 раз движутся в одну сторону и 50 раз в другую. Причем в эти промежутки электроны движутся не с постоянной скоростью. Их скорость плавно нарастает и плавно спадает.
- В-шестых, трехфазная система выделяется смещением обмоток фаз относительно друг друга на 120°. Это очень важно. Подробнее об этом будет рассмотрено далее.
Исходя из всего перечисленного можно отметить, что при переменном токе электроны подергиваются из стороны в сторону и практически не движутся. Однако электроны - это очень маленькие частицы. И если рассматривать их в разрезе атомов, то движение уже будет значительным.
Куда течет ток в четырехпроводной трехфазной цепи
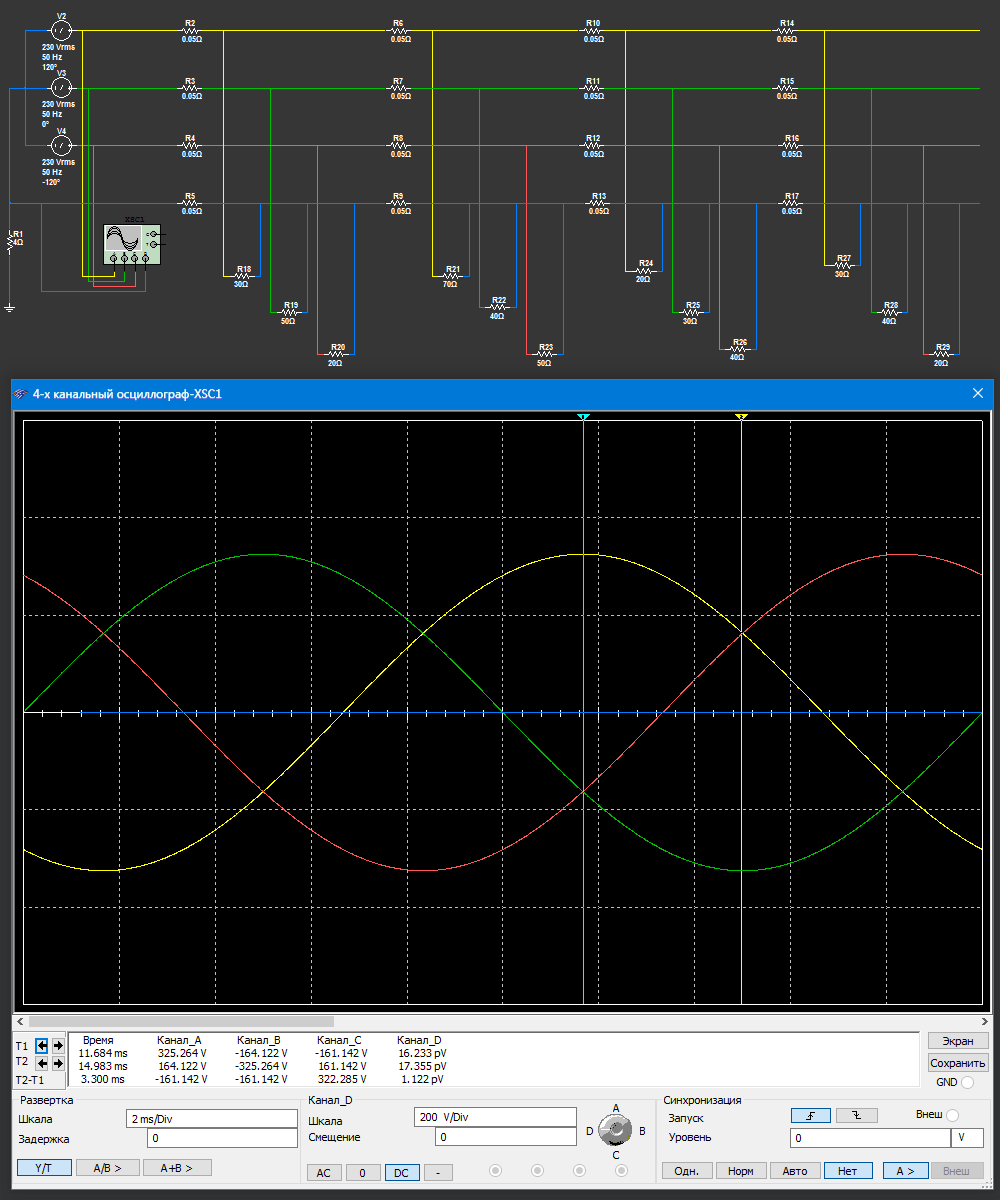
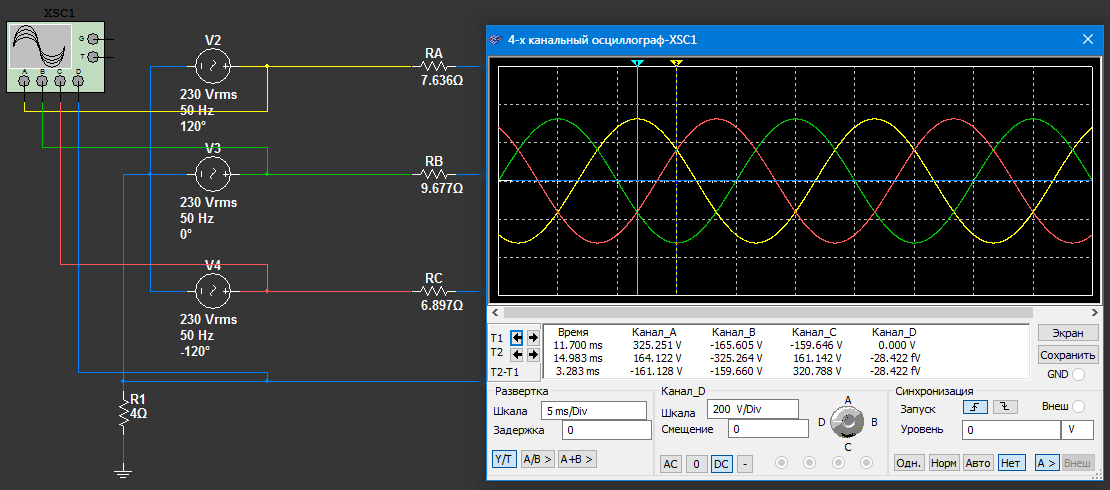
Ток (поток) - это непрерывное течение. В нашем случае ток - это упорядоченное движение свободных электронов в трехфазной цепи. Для движения электронов нужна разность потенциалов. Ее создает генератор. Точнее генератор создает одновременно разность потенциалов на концах трех фазных обмоток. И проанализировав эти потенциалы можно безошибочно определить направление движения тока. Давайте сделаем это воспользовавшись осциллографом и покажем направление течения тока в одной из фаз в определенный момент времени:
Что мы видим на схеме? Осциллограф подключен к выводам трех фаз и к нейтрали. Фазы отмечены желтым, зеленым и красным цветами. Нейтраль синим. На осциллографе мы взяли два момента времени, отмеченные голубым и желтым маркером. В эти моменты времени мы имеем следующие потенциалы на выводах генератора и нейтрали:
| Момент времени T1 | Момент времени T2 |
| Канал A (фаза - желтый цвет), потенциал ≈ +325 В | Канал A (фаза - желтый цвет), потенциал ≈ +164 В |
| Канал B (фаза - зеленый цвет), потенциал ≈ -164 В | Канал B (фаза - зеленый цвет), потенциал ≈ -325 В |
| Канал С (фаза - красный цвет), потенциал ≈ -161 В | Канал С (фаза - красный цвет), потенциал ≈ +161 В |
| Канал D (нейтраль - синий цвет), потенциал ≈ 0 В | Канал D (нейтраль - синий цвет), потенциал ≈ 0 В |
Какую можно проследить закономерность? Во-первых, потенциал нейтрали в любой момент времени практически равен нулю (это четко видно из графика). Почему потенциал нейтрали равен нулю - на этом чуть подробнее остановимся в одном из следующих пунктов. Во-вторых, сумма потенциалов на выводах трех фаз в любой момент времени тоже равна нулю. Сами же потенциалы выводов фаз изменяются во времени и их значения формируют график в виде синусоиды. Синусоиды каждой фазы одинаковы. Но они смещены друг относительно на 120°. Именно это смещение позволяет получить ноль при сложении потенциалов трех фаз в любой момент времени. Зачем нужен этот ноль и при чем здесь направление тока? Давайте разберемся наглядно.
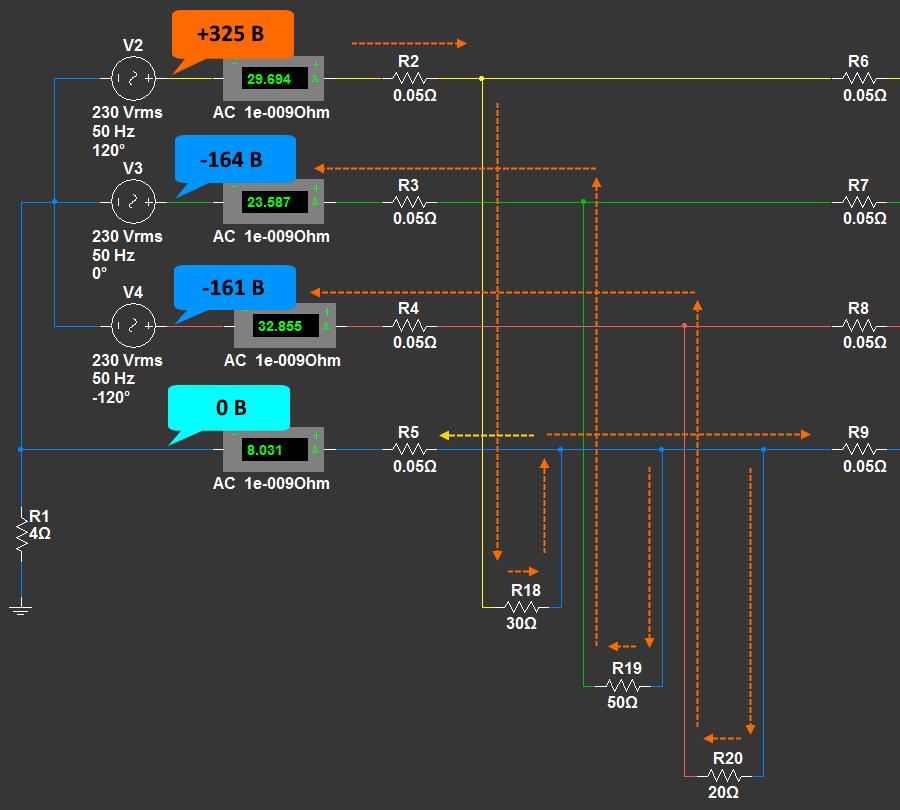
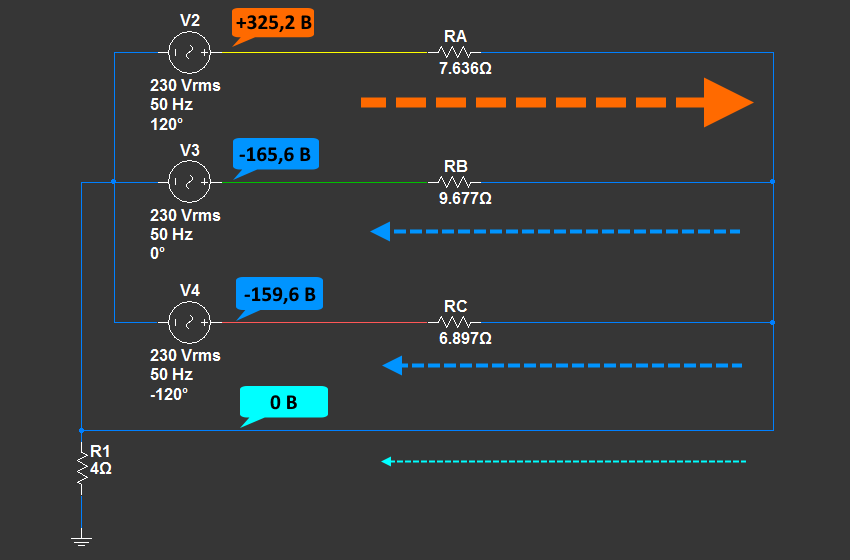
Рассмотрим момент времени T1, и для удобства перенесем потенциалы на схему цепи (для удобства показана только начальная часть схемы):
Ранее мы уже упоминали, что для движения электронов (тока) нужна разность потенциалов. В рассмотренный момент времени разность потенциалов есть между фазой A (желтая) и фазами B и C (зеленая и красная). На выводе фазы A имеется избыток положительных зарядов с потенциалом +325 В. На выводах фаз B и C имеется избыток отрицательных зарядов -164 В и -161 В (в сумме дают -325 В). Естественно заряды двинутся от большего потенциала к меньшему. 0 В на нейтрали значит, что разноименных зарядов поровну. При этом нулевой потенциал все же меньше +325 В, но это не значит, что по этому пути потекут заряды. Потенциал +325 В фазы A полностью компенсируется суммарным потенциалом -325 В фаз B и C. И все это благодаря смещению фазных обмоток друг относительно друга на 120°. Однако, если посмотреть на схему, то через ноль все же протекает ток (небольшая часть от основного тока, изображено желтой стрелкой). Этот интересный момент мы разберем позже на упрощенной схеме.
Теперь вернемся к схеме. На ней показано, что в момент времени T1 заряды от фазы A движутся к потребителям, сидящим на этой фазе. Далее по нулевому проводу возвращаются на общий нулевой провод идущий по опорам. Далее через нулевые провода идут к потребителям фаз B и C. Отсюда - к выводам фаз B и C. Небольшая часть зарядов возвращается в трансформатор по нулевому проводу.
На данном этапе хотелось бы отметить важную деталь. Мы показали, что движение начинают положительные заряды. На самом деле в металлах движутся только свободные электроны. А они заряжены отрицательно. Но так как принято брать направление тока от плюса к минусу, то мы будем придерживаться этого допущения.
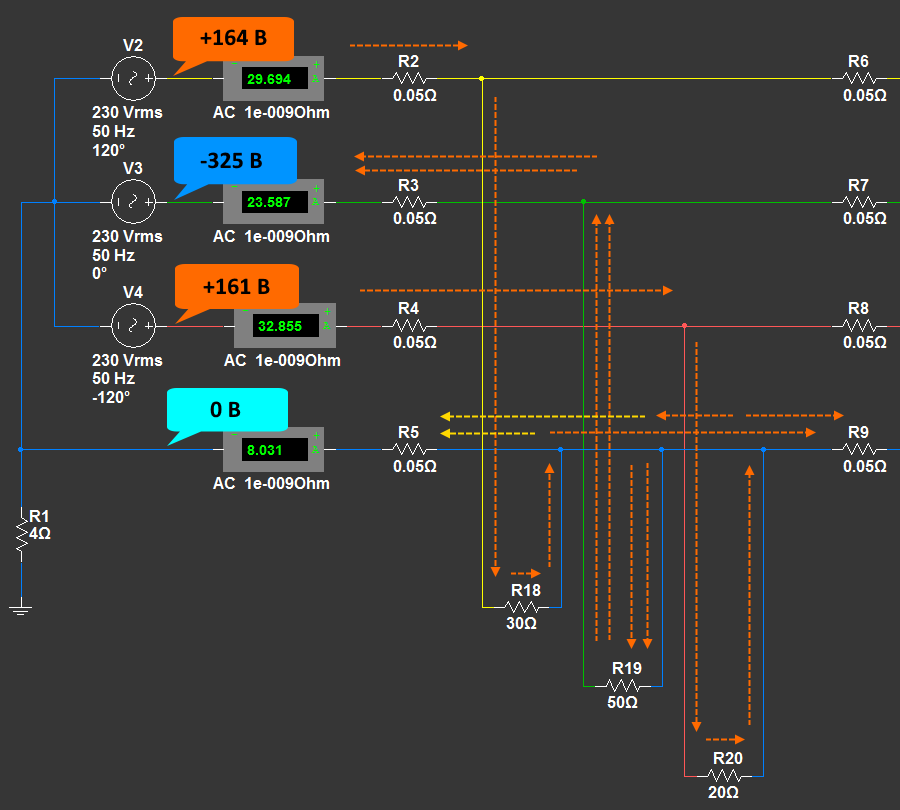
Рассмотрим момент времени T2, и для удобства перенесем потенциалы на схему цепи (для удобства показана только начальная часть схемы):
Анализируем пути протекания токов в момент времени T2 также по принципу - от большего потенциала к меньшему. В данном случае больший потенциал +325 В получается путем сложения потенциалов на выводах фаз A и C. Меньший потенциал -325 В на выводе В. На нейтрали так же как и в предыдущем случае потенциал 0 В.
В момент времени T2 заряды от фаз A и C движутся к потребителям, сидящим на этих фазах. Далее по нулевым проводам возвращаются на общий нулевой провод идущий по опорам. Далее через нулевые провода идут к потребителям фазы B. Отсюда - к выводу фазы B. Небольшая часть зарядов возвращается в трансформатор по нулевому проводу.
По такому же принципу можно проанализировать пути протекания токов в трехфазной цепи в любой момент времени.
Упрощенная схема движения токов в трехфазной цепи
Мы рассматривали движения токов в трехфазной цепи на примере электроснабжения улицы с домами. Схема получилась довольно разветвленной и сложной для восприятия. Давайте ее упростим.
В первую очередь избавимся от сопротивления проводов. Они у нас имели небольшое значение, которым можно пренебречь:
Теперь получившуюся схему можно представить в следующем виде:
Что первая, что вторая схема - они абсолютно идентичны. Просто по иному отрисованы. Нам нужно сложить сопротивления на каждой фазе. И именно вторая схема оптимальна для этого, так как визуально более понятна для восприятия. Каждая нагрузка (сопротивление) соединена одновременно с фазой и нулем. Такое соединение нескольких резисторов при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов называется параллельным и имеет свои особенности при расчете общего сопротивления.
Эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn.
Рассчитаем общее сопротивление для фазы A:
1 / RA = 1 / R18 + 1 / R21 + 1 / R24 + 1 / R27 = 1 / 30 ом + 1 / 70 ом + 1 / 20 ом + 1 / 30 ом = (7+3+10,5+7) / 210 = 27,5 / 210; R = 210 / 27,5 = 7,636 ом.
Аналогично рассчитываем общее сопротивление по фазам B и С. Получаем следующую схему:
Согласитесь, так намного проще анализировать движение токов в трехфазной цепи.
Как и ранее прибегнем к помощи осциллографа:
На осциллографе мы взяли два момента времени, отмеченные голубым и желтым маркером. В эти моменты времени мы имеем следующие потенциалы на выводах генератора и нейтрали:
| Момент времени T1 | Момент времени T2 |
| Канал A (фаза - желтый цвет), потенциал ≈ +325,2 В | Канал A (фаза - желтый цвет), потенциал ≈ +164 В |
| Канал B (фаза - зеленый цвет), потенциал ≈ -165,6 В | Канал B (фаза - зеленый цвет), потенциал ≈ -325 В |
| Канал С (фаза - красный цвет), потенциал ≈ -159,6 В | Канал С (фаза - красный цвет), потенциал ≈ +161 В |
| Канал D (нейтраль - синий цвет), потенциал ≈ 0 В | Канал D (нейтраль - синий цвет), потенциал ≈ 0 В |
Здесь мы видим такую же закономерность - потенциал нейтрали в любой момент времени практически равен нулю, и сумма потенциалов на выводах трех фаз в любой момент времени тоже равна нулю.
Как и в предыдущих случаях перенесем потенциалы на схему и покажем направления движения токов в момент времени T1:
В момент времени T1 на выводе фазы А скапливается некоторое количество заряда, формирующее потенциал +325,2 В. В тот же момент на выводах B и C суммарно имеется такое же количество зарядов, только со знаком «минус». В цепи образуется электрическое поле и заряды устремляются от плюса к минусу. Логично, что положительные заряды от фазы A должны направится к фазам B и C, где имеется такое же количество отрицательных зарядов. Однако некоторое количество зарядов все же возвращается в трансформатор по нулевому проводу. Это мы можем наглядно увидеть на следующей схеме, в которую добавлены амперметры:
Заряды, двигающиеся по нулевому проводу создают в нем ток с действующим значением 8,4 А.
Нужно понимать, что когда мы рассматриваем потенциалы (напряжения) полученные с осциллографа, то эти значения мгновенные (амплитудные на вершинах синусоиды). Когда же мы снимаем показания с вольтметра и амперметра, то эти значения действующие. Важно не запутаться и четко разделять действующие и мгновенные (амплитудные) значения напряжения и тока.
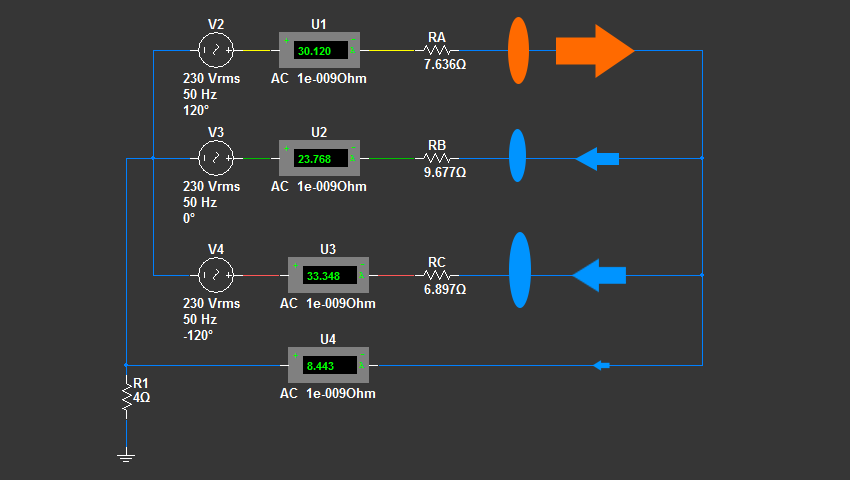
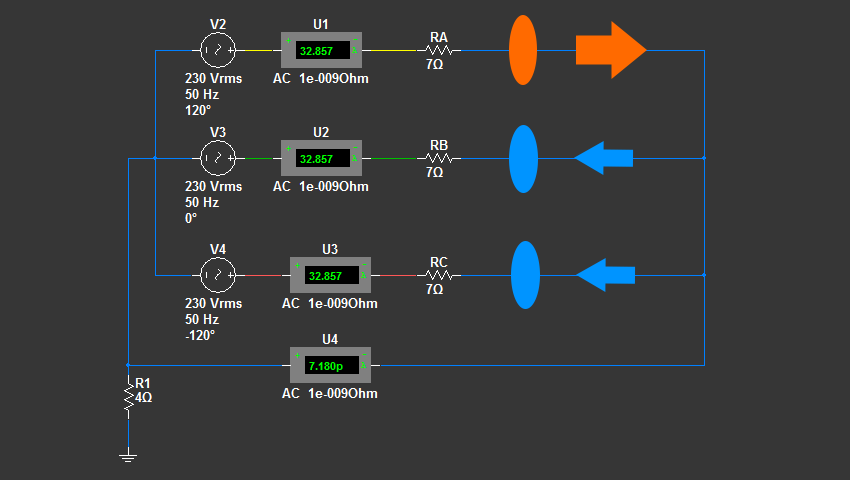
Давайте разберемся, почему же заряды пошли по нулевому проводу. На самом деле - все просто. В цепи на каждой фазе у нас имеется нагрузка. Причем сопротивления нагрузок несимметричные. Сопротивление - это препятствие на пути зарядов. Можно привести следующую аналогию - чем больше сопротивление, тем меньше «дверь» - пространство, через которое проходят заряды. Чтобы это лучше понять, вначале сделаем симметричную нагрузку по фазам. Для этого зададим одинаковое сопротивление резисторам RA, RB и RC равное 7 ом:
Получаем по фазам одинаковые по размеру двери для прохода зарядов. Итак, из фазы A в момент времени T1 вылетает n-е количество зарядов и проходит через дверь RA (7 ом). После этого заряды разделяются условно пополам и возвращаются в трансформатор через двери RB и RC такого же размера, как и дверь RA. Может возникнуть вопрос, зачем делать все двери одинакового размера, если в каждую из двух последних проходит зарядов в двое меньше. Все дело в том, что мгновенные напряжения на резисторах RB и RC условно в два раза меньше на резисторе RA. Соответственно и ток в два раза меньше. Поэтому, чтобы заряды без скоплений продвигались по цепи, нужно чтобы все двери были одинакового размера.
Еще раз подчеркну - даже при симметричной нагрузке мгновенные напряжения и токи по фазам могут, а точнее, будут отличатся. А действующие значения будут равны (как видно из показаний амперметров).
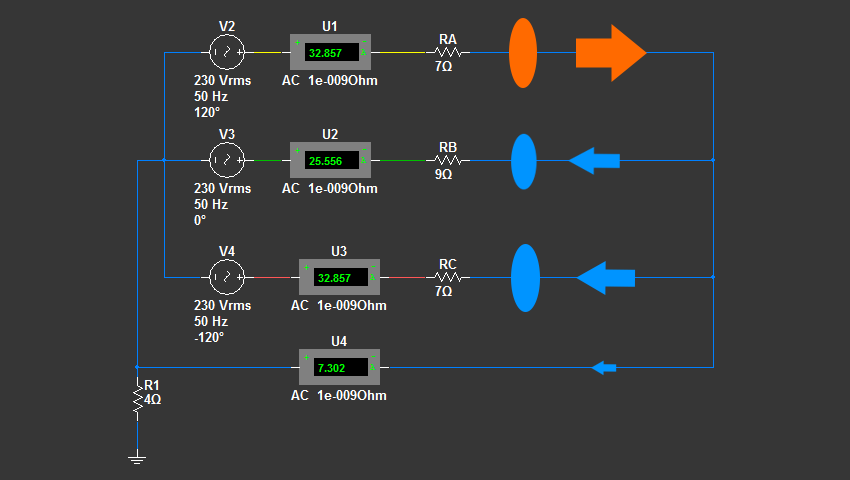
Теперь уменьшим дверь на фазе B и посмотрим, что произойдет:
Из фазы A в момент времени T1 вылетает n-е количество зарядов и проходит через дверь RA (7 ом). После этого заряды разделяются условно пополам и возвращаются в трансформатор через двери RB и RC. Дверь RC такого же размера, как и дверь RA. Поэтому условная половина зарядов беспрепятственно возвращается через нее в трансформатор. А вот дверь RB уже поменьше (9 ом), и условная половина зарядов физически не может вернуться в трансформатор в отведенное для этого время. Такую несимметрию (разную нагрузку - сечение для прохода зарядов) компенсирует нулевой провод. И именно по нему возвращается в трансформатор та часть зарядов, которая не смогла протиснуться в узкую дверь RB. На схеме это наглядно видно по амперметру, показывающему ток в нулевом проводе. В данном примере ток в фазах A и С одинаковый 32,8 А. Ток в фазе B 25,5 А. Ток в нулевом проводе 7,3 А. Сложив токи в фазе B и нулевом проводе получим 32,8 А.
Почему потенциал нейтрали 0 В
Разобравшись с мгновенными значениями и направлениями токов в трехфазной цепи, вернемся к вопросу, почему потенциал нейтрали 0 В.
Сразу хочется отметить, что не всегда на нейтрали трансформатора бывает нулевой потенциал. Но эти редкие случаи сейчас рассматривать не будем.
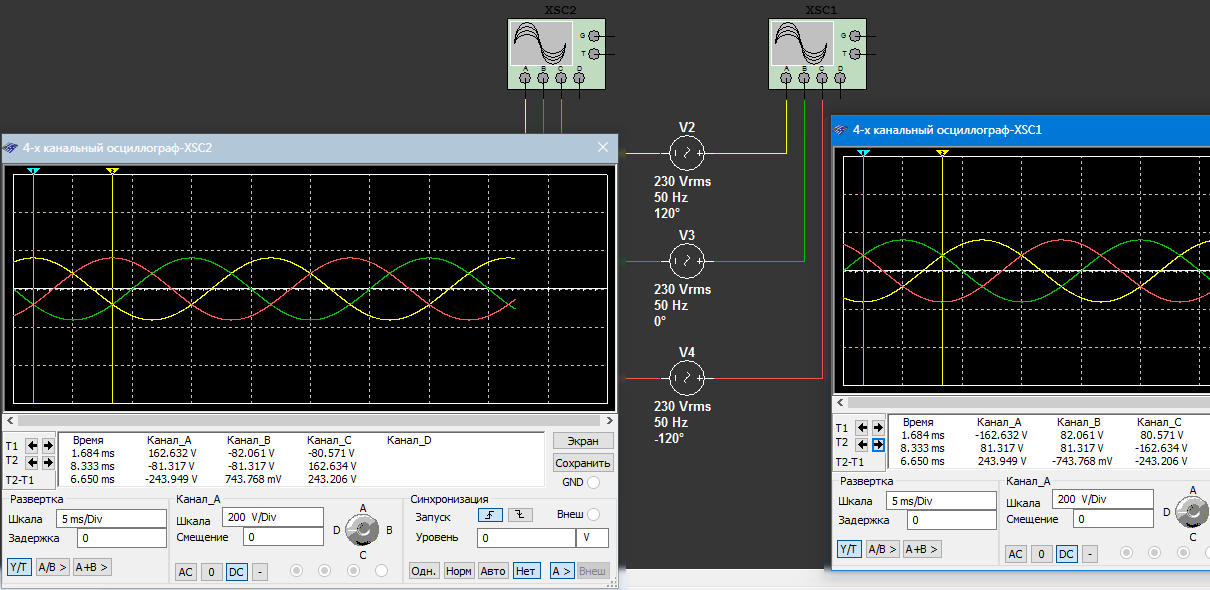
Начнем с того, что возьмем три однофазных генератора, имеющих друг относительно друга смещение фазных обмоток на 120°. Подключим к их выводам осциллографы и проанализируем потенциалы в определенные моменты времени:
| Момент времени T1 конец обмотки | Момент времени T1 начало обмотки |
| Канал A (фаза - желтый цвет), потенциал ≈ +162,6 В | Канал A (фаза - желтый цвет), потенциал ≈ -162,6 В |
| Канал B (фаза - зеленый цвет), потенциал ≈ -82 В | Канал B (фаза - зеленый цвет), потенциал ≈ +82 В |
| Канал С (фаза - красный цвет), потенциал ≈ -80,6 В | Канал С (фаза - красный цвет), потенциал ≈ +80,6 В |
| Момент времени T2 конец обмотки | Момент времени T2 начало обмотки |
| Канал A (фаза - желтый цвет), потенциал ≈ -81,3 В | Канал A (фаза - желтый цвет), потенциал ≈ +81,3 В |
| Канал B (фаза - зеленый цвет), потенциал ≈ -81,3 В | Канал B (фаза - зеленый цвет), потенциал ≈ +81,3 В |
| Канал С (фаза - красный цвет), потенциал ≈ +162,6 В | Канал С (фаза - красный цвет), потенциал ≈ -162,6 В |
Нейтраль (ноль) трансформатора - это точка, в которой концы обмоток всех трех фаз (А, В, С) соединяются вместе. Покажем это на схеме:
Чтобы найти потенциал нейтрали трансформатора, нужно сложить потенциалы на концах фазных обмоток. Сделаем это для момента времени T1 и T2:
- Потенциал на конце фазной обмотки (A) +162,6 В. То есть здесь имеется избыток зарядов. Потенциал на конце фазной обмотки (B) -81,3 В. Потенциал на конце фазной обмотки (C) -80,6 В. На двух других концах имеется недостаток зарядов, дающий суммарно -162,6 В. Сложив эти потенциалы получаем 0 В.
- Аналогично для момента времени T2 (и всех моментов времени). Сложение потенциалов даст 0 В.
Условное направление токов в трехфазной цепи
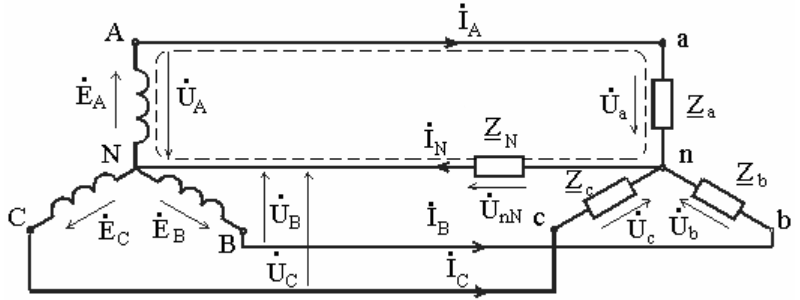
Рассматриваемая нами цепь является четырехпроводной и по-научному называется - схема соединения фаз источника и приемника в звезду.
Схема соединения фаз источника и приемника в звезду:
 В литературе по теоретическим основам электроустановок, как правило, все сведено к математическому упрощению. Трехфазная система ЭДС может изображаться тригонометрическими функциями, функциями комплексного переменного, графиками на временных диаграммах, векторами на векторных диаграммах. Такое упрощение может сыграть со многими злую шутку. Некоторые могут не до конца разобраться или вовсе не понять такое векторное представление. В результате начинается неправильная трактовка очевидных фактов. Я нередко сталкивался с таким недопониманием. Многие с уверенностью доказывают, что ток от фазы по нулевому (нейтральному) проводу возвращается в трансформатор. И спорить с ними очень трудно.
В литературе по теоретическим основам электроустановок, как правило, все сведено к математическому упрощению. Трехфазная система ЭДС может изображаться тригонометрическими функциями, функциями комплексного переменного, графиками на временных диаграммах, векторами на векторных диаграммах. Такое упрощение может сыграть со многими злую шутку. Некоторые могут не до конца разобраться или вовсе не понять такое векторное представление. В результате начинается неправильная трактовка очевидных фактов. Я нередко сталкивался с таким недопониманием. Многие с уверенностью доказывают, что ток от фазы по нулевому (нейтральному) проводу возвращается в трансформатор. И спорить с ними очень трудно.
Но даже в такой литературе есть довольно понятные ответы. Если рассмотреть векторную диаграмму напряжений и токов при соединении фаз симметричного приемника в звезду, то ток в нейтральном проводе равен I’n = I’a+I’b+I’c = 0. Следовательно, при соединении в звезду фаз симметричного приемника нейтральный провод не оказывает влияния на работу цепи и может быть исключен. То есть по нему не течет ток. Все токи распределяются между фазами.
Естественно конечные потребители (дома) не являются симметричным приемником. Хотя при распределении фаз стремятся добиться симметрии. Поэтому здесь нужен нулевой (нейтральный провод), по которому к трансформатору протекает часть тока, появившегося в результате несимметрии.