Содержание записи:

Ферма — конструкция, определение усилий

Фермы как конструкции широко используются при строительстве мостов, мостовых пролетов, перекрытий зданий, ангаров. Перекрытия из ферм имеют неоспоримые преимущества в случаях, когда требуется перекрыть пролеты величиной несколько десятков метров, что невозможно сделать при помощи сплошных балок. При этом использование фермы вместо сплошной балки потребует значительно меньшего количества металла, и, следовательно, в разы снизится и вес всей конструкции.

Классификация ферм

Ферма — это жесткая (геометрически неизменяемая) конструкция из прямолинейных стержней, которые соединены между собой по концам с помощью шарниров.

По материалу изготовления фермы классифицируются на:

Металлические.
Деревянные.
Металлодеревянные.
Железобетонные.

По типу решетки выделяют фермы:

С раскосной решеткой. Раскосы, идущие вверх от опор к середине фермы, называют восходящими раскосами, идущие наоборот — нисходящими раскосами.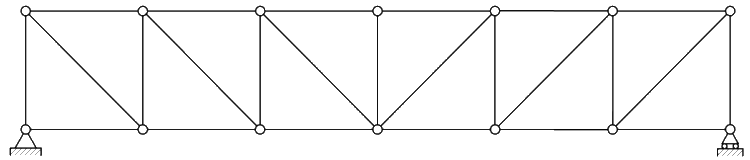
С треугольной решеткой.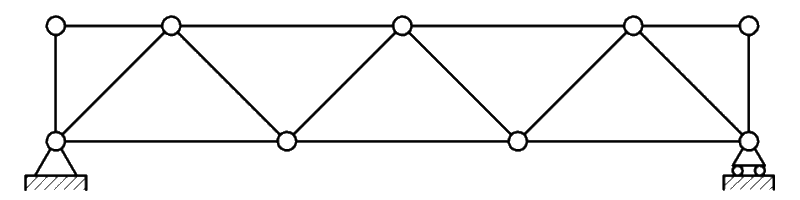
Усиленные дополнительными стержнями (шпренгелями). Наличие шпренгелей позволяет увеличить количество узлов в этом поясе, что может потребоваться для облегчения конструкций, с помощью которых внешняя нагрузка передается на узлы фермы, или, например, для уменьшения ширины плит перекрытий, опирающихся на стропильные фермы здания.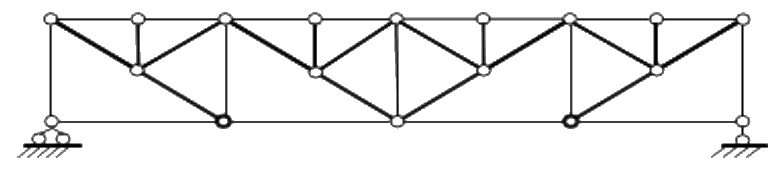

По направлению опорных реакций фермы бывают:

Балочные.	К таким фермам относятся конструкции с раскосой треугольной решеткой и усиленные шпренгелями (смотреть предыдущий пункт).
Консольные фермы.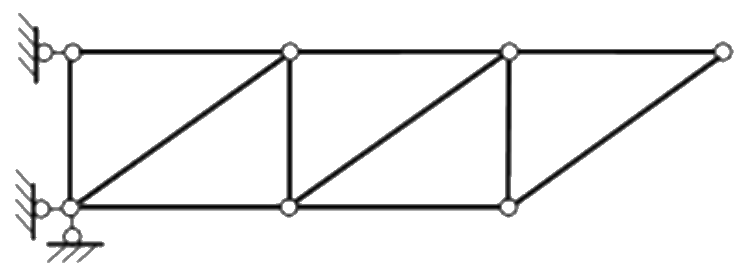
Консольно балочные.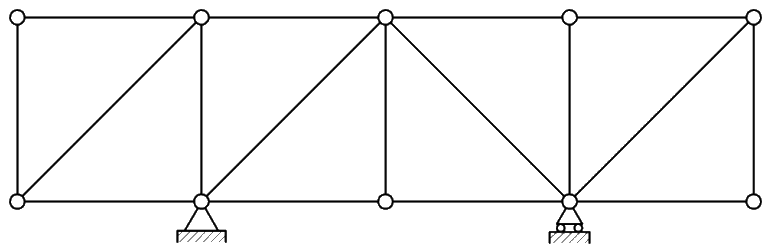
Арочные.

По очертанию поясов выделяют:

Фермы с параллельными поясами.
Фермы ломаного очертания.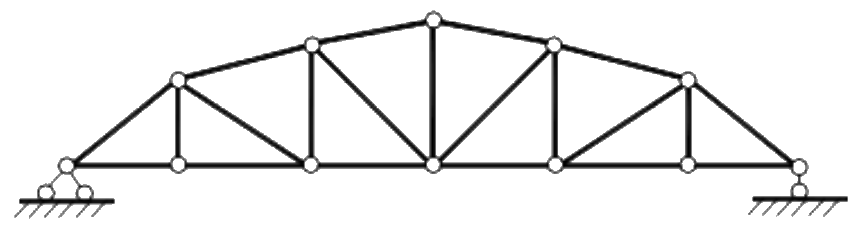
Треугольные фермы.
Фермы криволинейного очертания, в которых узлы верхнего или нижнего пояса, или обоих поясов, располагаются по кривой, однако сами стержни обязательно прямые.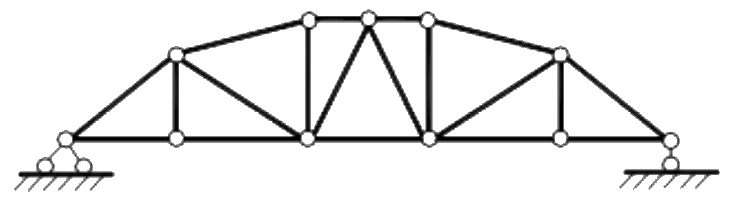
Полураскосные фермы. В таких конструкциях раскосы идут не от пояса к поясу, а от поясов к середине стоек.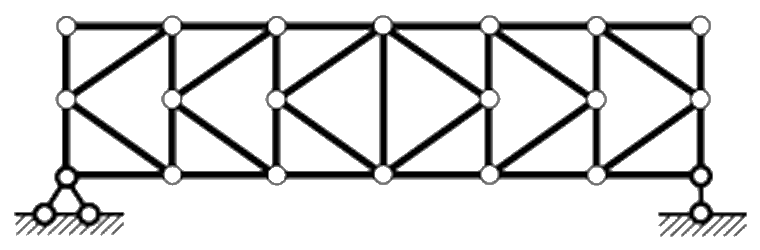

Плоская ферма

Плоская ферма — это конструкция, у которой оси всех стержней принадлежат одной плоскости.

Простой плоской фермой называется ферма, которая может быть получена из треугольной путем последовательного присоединения каждого нового узла с помощью двух новых стержней.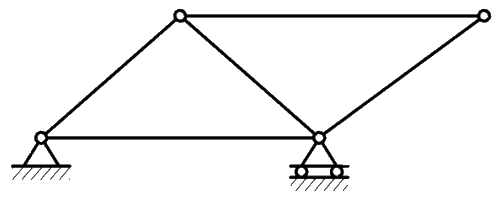

Основные элементы ферм:

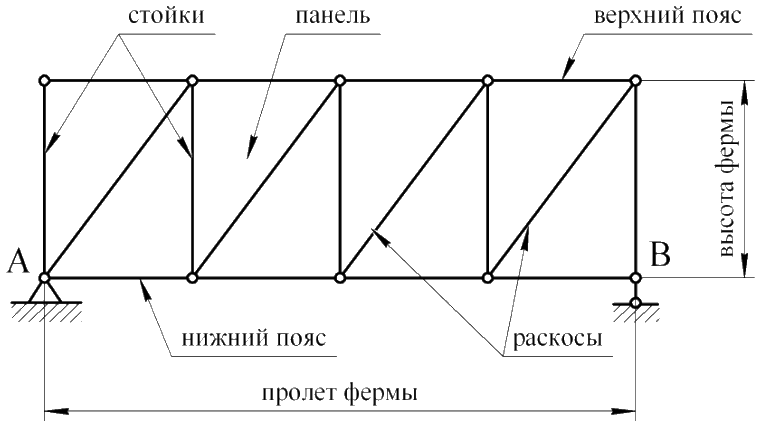Узлы фермы — это точки соединения стержней фермы.

Расстояние между двумя соседними узлами любого из поясов фермы
называется панелью фермы.

Опорные узлы — это узлы фермы, которыми она опирается на основу.

Верхний (нижний) пояс фермы — стержни, расположенные по верхнему (нижнему) контуру фермы.

Расстояние между осями поясов — это высота фермы.

Стойки — вертикальные стержни фермы.

Раскосы — это наклонные стержни фермы.

Совокупность раскосов и стоек образует решетку фермы.

Нулевые стержни — это стержни, в которых усилия приравнивают нулю.

Плоские фермы проектируются таким образом, что приложенная к конструкции нагрузка передается в узлах, вследствие чего в сечениях элементов ферм не возникают поперечные силы и изгибающие моменты, стержень работает только на продольные усилия (растяжение или сжатие). Таким образом, реакции стержней фермы будут направлены вдоль этих стержней.

Для обеспечения жесткости конструкции плоской фермы необходимо, чтобы число узлов «n» и число стержней «m» удовлетворяли следующему уравнению: m = 2n — 3. Если число стержней m < 2n — 3, то конструкция не обладает жесткостью, а при числе стержней m > 2n — 3 ферма будет избыточно жесткой.

Расчет ферм под действием неподвижной нагрузки

Основной целью статического расчета фермы является определение усилий в ее стержнях. По этим усилиям в дальнейшем производят подбор сечений элементов фермы и расчет узловых креплений элементов. Рассмотрим методы для определения усилий в стержнях фермы под действием неподвижных нагрузок.

Метод вырезания узлов

Метод вырезания узлов предполагает последовательное мысленное вырезание узлов фермы, к которым прилагаются соответствующие внешние силы и реакции стержней. Расчет начинается с узла, в котором соединяются два стержня. Каждый следующий узел выбирается так, чтоб с ним совпадало не больше двух стержней с неизвестными реакциями.

Пример выбора узлов:

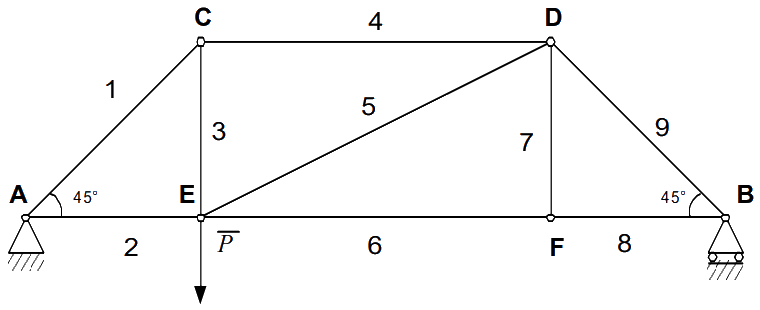Стержни, которые совпадают в узлах фермы, являются связями для узлового соединения. Мысленно откинем связи и заменим их действие на узлы реакциями связей:

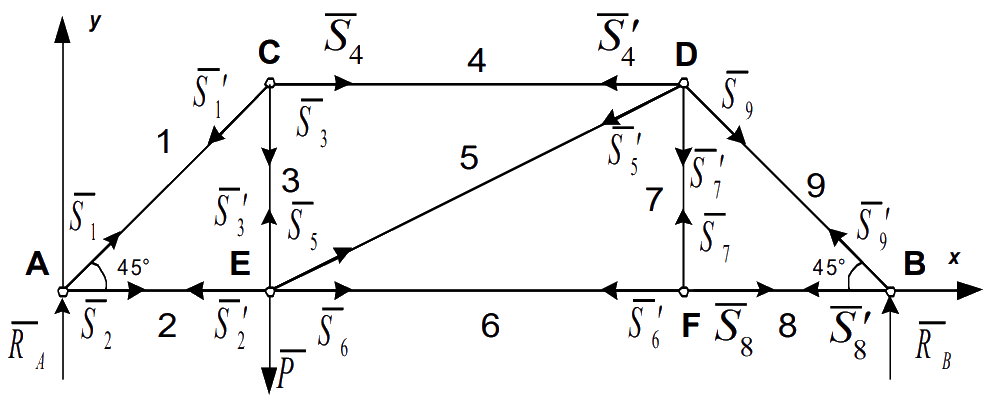Сначала неизвестно, какие из стержней фермы растянуты, а какие сжаты. Поэтому условно считается, что все стержни растянуты и реакции имеют направление от узлов. Если при вычислениях получится ответ отрицательный, то это означает, что соответствующий стержень сжат. Найденные реакции стержней по модулю равны внутренним усилиям в стержнях.

Используя следующие леммы, можно без расчетов определить нулевые стержни:

Если к ненагруженному узлу плоской фермы сходятся два стержня, то усилия в этих стержнях равно нулю.
Если к ненагруженному узлу плоской фермы сходятся три стержня, из которых два расположены на одной прямой, то усилие в третьем стержне равно нулю. Усилие в первых двух стержнях равны.
Если к узлу плоской фермы сходятся два стержня и в этом узле приложенная сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне равно по модулю приложенной силы, а усилие в другом стержне равно нулю.

Вырезая узел, получается плоская сходящаяся система сил. Для решения задачи может быть применен аналитический или графический метод. В случае аналитического метода составляется два уравнения равновесия в виде: {∑F_kx = 0; ∑F_kx = 0.

В случае графического метода строится многоугольник сил, которые приложены к узлу. Этот многоугольник должен быть замкнут. При построении этого многоугольника нужно откладывать известные силы в соответствии с их действительным направлением. Если построить силовой многоугольник не для отдельного узла, а для всей фермы в целом по соответствующим правилам, то получится диаграмма Максвелла-Кремоны.

Метод вырезания узлов удобно использовать, когда нужно определить усилия во всех стержнях фермы. При этом последующие реакции определяются через предыдущие.

Метод сечений

Метод сечений предполагает мысленное разделение фермы на две части сечением, которое проходит через три стержня, в которых (или в одном из них) нужно определить усилия, и рассматривается равновесие одной из частей. Действие отброшенной части заменяется соответствующими силами, которые имеют направление вдоль перерезанных стержней от узлов, то есть, считая стержни растянутыми, как и в методе вырезания узлов.

Следующим шагом составляется уравнение равновесия полученной плоской произвольной системы сил (реакции опор должны быть найденные заранее). Наиболее эффективно использование
метода моментных точек (метод Риттера), согласно которому составляются уравнения моментов сил относительно моментных точек Риттера (точек в которых пересекаются два других стержня):

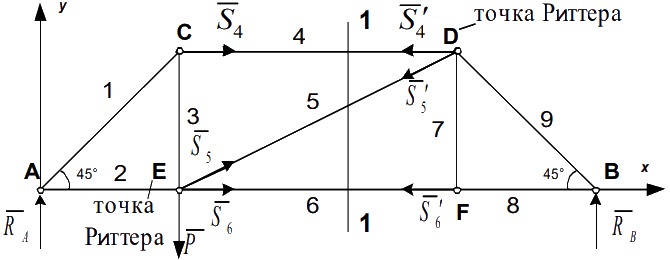Для определения усилия S₄ точкой Риттера будет узел E, а для определения усилия S₆ точкой Риттера будет узел D. В случае, когда моментная точка не существует (находится в бесконечности), то есть когда стержни фермы параллельные, используется метод проекций. Согласно этому методу составляется уравнения проекций сил на ось, которая перпендикулярна параллельным стержням фермы (для определения усилия S₅).

Метод сечений удобно использовать, когда нужно обнаружить усилия в отдельных стержнях. Он позволяет обнаружить усилия в произвольном стержне фермы независимо от усилий в других стержнях.

Метод линий влияния

Используя метод линий влияния, ферма нагружается единичной силой, которая двигается вдоль пояса, по которому двигается реальная нагрузка (нагрузка передается через узлы). Для этого используется метод сечений (удобнее) или метод вырезания узлов, и находятся усилия в стержне, который исследуется.

Различают два способа построения линий влияния:

Определяется зависимость, которая связывает усилие со сменной координатой точки приложения единичной силы, и строится график этой зависимости.
Определяется зависимость, которая связывает усилие с усилиями других стержней, для которых линии влияния уже известны, а потом путем достижения и добавления этих графиков строится график линии влияния.

При применении метода сечений нужно рассматривать случаи, когда сила находится справа и слева от этого стержня. Когда сечение расположено между узлами, то если сила приложена слева от сечения, рассматривается правая часть фермы, и, наоборот, когда сила справа от сечения — левая часть фермы. В случае, когда сечение расположено на консоли, всегда рассматривается консольная часть. Полученные выражения строятся в виде графиков и соединяются крайние ординаты левого и правого участков прямой. Получается линия влияния стержня. Для построения или для проверки можно использовать свойство линий влияния (левая и правая часть линий влияния пересекается под точкой Риттера).

При применении метода вырезания узлов (чаще всего — для стоек) нужно рассмотреть случаи, когда сила приложена в узле и вне узла. Иногда сначала необходимо построить линию влияния стержней, которые соединены из исследуемых стержней.

В случае, когда нагрузка на ферму передается с помощью поперечных балок (узловая передача нагрузки), необходимо на линии влияния, которая построена для непосредственной нагрузки, спроектировать узлы пояса фермы и соединить полученные точки прямыми линиями.

Для линии влияния раскосов имеет место правило знаков: так как верхний пояс сжат, а нижний растянут, и отрицательные ординаты отложены от оси абсцисс вниз, а положительные — вверх, то соединительная прямая имеет наклон, противоположный наклону раскоса.

Линии влияния для поясов и раскосов фермы, которые имеют стойки, не изменяются при изменении движения нагрузки понизу движением по верхнему поясу и наоборот. В этом случае изменяются только линии влияния в стойках.

Пример линий влияния стержней фермы:

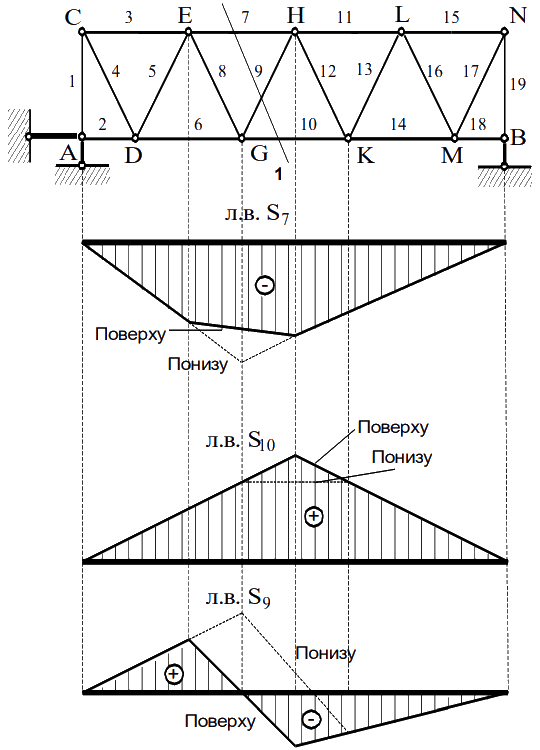Когда ферма состоит только из стержней, которые имеют наклон, то переход нагрузки с нижнего пояса на верхний или наоборот отображается на всех линиях влияния.