Закон Ома - калькулятор, формулы, методика расчета

Закон Ома - эмпирический физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь.
В данном обзоре приведены программы и калькуляторы закона Ома. Также дополнительно приведены основные формулы и методики расчетов.
Закон Ома - калькулятор онлайн
Онлайн калькулятор закона Ома позволяет быстро просчитать основные переменные для участка цепи. Для этого вам необходимо ввести любые два известных значения и нажать «рассчитать».
| U Напряжение (В): | |
| P Мощность (Вт): | |
| R Сопротивление (Ом): | |
| I Сила тока (А): | |
Закон Ома для постоянного тока - расчет, формулы
Закон Ома для постоянного тока определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи.
Закон Ома для полной цепи:
I = ε / (R + r), где:
- ε - ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Из закона Ома для полной цепи вытекают следующие следствия:
- При r < R сила тока в цепи обратно пропорциональна ее сопротивлению, а сам источник в ряде случаев может быть назван источником напряжения.
- При r > R сила тока не зависит от свойств внешней цепи (величины нагрузки), и источник может быть назван источником тока.
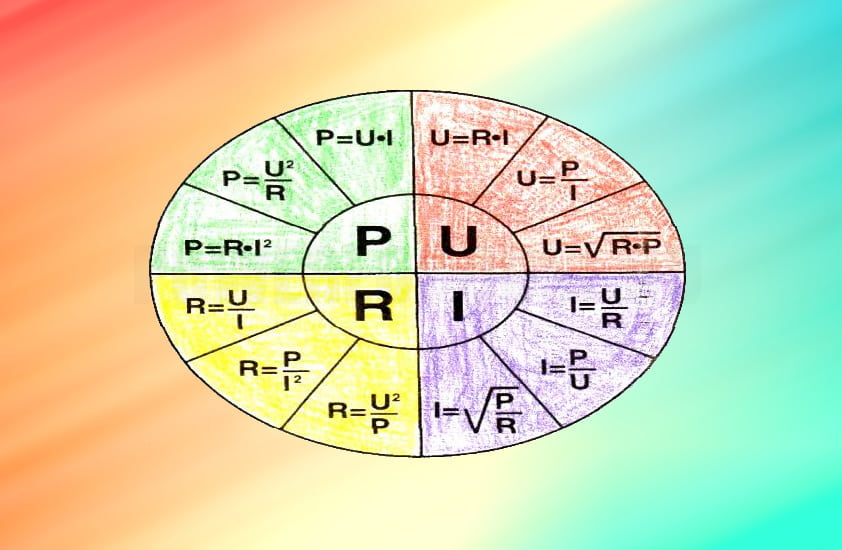
Часто выражение I = U / R тоже называют законом Ома. При этом формулировка следующая - сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, где:
- I - сила тока, измеряемая в Амперах (A).
- U - напряжение, измеряемое в Вольтах (V).
- R - сопротивление, измеряемое в Омах (Ом, Ω).
Помимо закона Ома, важнейшим является понятие электрической мощности. Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U):
P = I × U, где:
- P - электрическая мощность, измеряемая в Ваттах (W).
- I - сила тока, измеряемая в Амперах (A).
- U - напряжение, измеряемое в Вольтах (V).
Комбинируя две формулы можно получить зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
Множительные приставки в системе СИ примирительные к закону Ома:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А; 1 миллиампер (1 mA) = 0,001 A; 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V; 1 милливольт (1 mV) = 0,001 V; 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Ом): 1 мегаом (1 MОм) = 1000000 Ом; 1 килоом (1 kОм) = 1000 Ом.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W; 1 киловатт (1 kW) = 1000 W; 1 милливатт (1 mW) = 0,001 W.
Закон Ома для цепи переменного тока
В цепи переменного тока сопротивление кроме активной, может иметь как емкостную, так и индуктивную составляющие. Рассмотрим цепь переменного тока, состоящую из резистора сопротивлением R, конденсатора емкостью C и катушки индуктивностью L, соединенных последовательно.
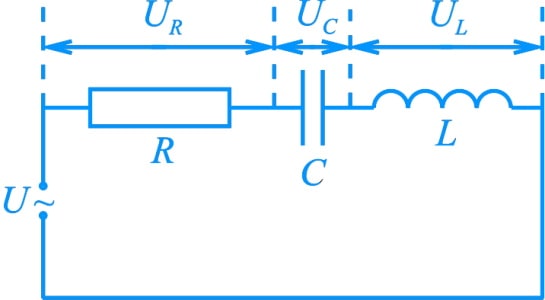
Мгновенные значения силы тока на всех элементах этой цепи одинаковы, а мгновенное значение напряжения между концами цепи равно алгебраической сумме мгновенных значений напряжений на резисторе (UR), конденсаторе (UC) и катушке индуктивности (UL).
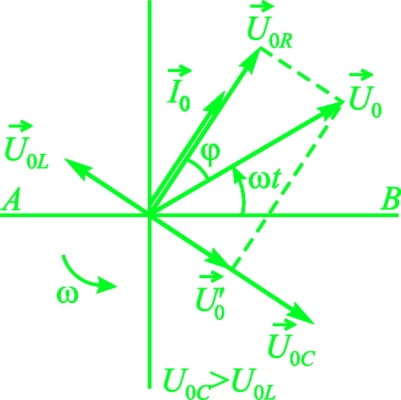
Для того чтобы определить амплитудные (или действующие) значения напряжения и силы тока, а также сдвиг фаз между ними удобно использовать метод векторных диаграмм. Здесь действующие значения всех напряжений и токов рассматриваются как векторы, вращающиеся с угловой скоростью ω, равной циклической частоте переменного тока, а их мгновенные значения определяются проекциями этих векторов на горизонтальную ось. Так как сила тока в цепи одинакова, то построение векторной диаграммы начинается с вектора I¯0, модуль которого равен амплитудному значению силы тока в цепи. Направление этого вектора может быть любым. Зададим угол α = ωt к горизонтали.
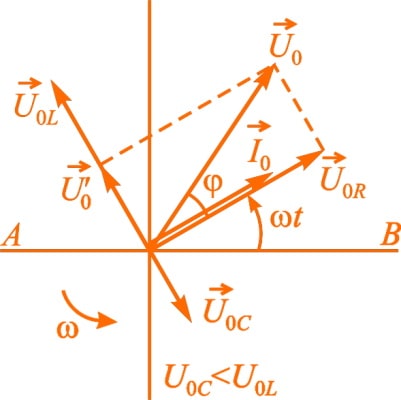
Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, поэтому вектор U¯0R, модуль которого равен U0R = I0 × R, совпадает по направлению с вектором I¯0. Сдвиг фаз между колебаниями силы тока и колебаниями напряжения на индуктивном сопротивлении составляет π / 2, причем ток отстает по фазе от напряжения. Поэтому вектор U¯0L, модуль которого равен U0L = I0 × ωL, нужно повернуть относительно вектора I¯0 на угол π / 2 против часовой стрелки. Вектор U¯0C, модуль которого равен I0 / ωC, отстает по фазе от вектора I¯0 на π / 2, поэтому его нужно повернуть на этот угол по часовой стрелке.
Для того чтобы найти напряжение на зажимах цепи, необходимо сложить три вектора: U¯0 = U¯0R + U¯0L + U¯0C.
В первую очередь сложим векторы U¯0R и U¯0C. Модуль этой суммы U'0 = [U¯0R + U¯0C]. Пусть ωL > 1 / ωC, тогда: U'0 = I0 × (ωL - 1 / ωC).
Теперь сложим векторы U¯0R и U'¯0. Модуль вектора U¯0 определяется по теореме Пифагора: U0² = U0R² + (U0L - U0C)² = I0² × R² + I0² × (ωL - 1 / ωC)². Соответственно амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению (закон Ома для цепи переменного тока):
I0 = U0 / √(R² + (ωL - 1 / ωC)²) = U0 / Z, где:
- Z - полное сопротивление (импеданс) цепи.
- R - его активное сопротивление.
- ωL - 1 / ωC - реактивное сопротивление цепи переменного тока.
- ω = 2 × π × γ - циклическая, угловая частота. γ - частота переменного тока.
Импеданс при параллельном подключении Z = 1 / √(1 / R² + 1 / (1 / ωL - ωC)²).
Сдвиг фаз между силой тока и напряжением равен углу φ между векторами U¯0 и I¯0. В соответствии с графиком выше ток отстает от напряжения на угол φ, причем tgφ = (ωL - 1 / ωC) / R.
Для того чтобы определить мгновенные значения напряжений на активном, емкостном и индуктивном сопротивлениях, необходимо спроектировать векторы U¯0R, U¯0L, U¯0C на прямую АВ.
Тогда:
- UR = I0 × R × sin × (ωt + φ).
- UL = I0 × ωL × sin × (ωt + φ + π / 2).
- UC = (I0 / ωС) × sin × (ωt + φ - π / 2).
Если 1 / ωС > ωL, то:
- U'0 = I0 × (1 / ωС - ωL).
- tgφ = (1 / ωC - ωL) / R, причем ток опережает напряжение по фазе на угол φ.
Таблица удельных сопротивлений проводников
Электрическое сопротивление (ρ) 1 метра провода, сечением 1 мм², при температуре 20 С°:
| Материал проводника | Удельное сопротивление ρ, Ом |
| Серебро | 0.015 |
| Медь | 0.0175 |
| Золото | 0.023 |
| Латунь | 0,025. 0,108 |
| Хром | 0,027 |
| Алюминий | 0.028 |
| Натрий | 0.047 |
| Иридий | 0.0474 |
| Вольфрам | 0.05 |
| Цинк | 0.054 |
| Молибден | 0.059 |
| Никель | 0.087 |
| Бронза | 0,095. 0,1 |
| Железо | 0.1 |
| Сталь | 0,103. 0,137 |
| Олово | 0.12 |
| Свинец | 0.22 |
| Никелин (сплав меди, никеля и цинка) | 0.42 |
| Манганин (сплав меди, никеля и марганца) | 0,43. 0,51 |
| Константан (сплав меди, никеля и алюминия) | 0,44-0,52 |
| Копель (медно-никелевый сплав с 43% никеля и 0,5% марганца) | 0.5 |
| Титан | 0.6 |
| Ртуть | 0.94 |
| Хромель (хром 8,7 - 10 %; никель 89 - 91 %; кремний, медь, марганец, кобальт - примеси) | 1.01 |
| Нихром (сплав никеля, хрома, железа и марганца) | 1,05. 1,4 |
| Фехраль | 1,15. 1,35 |
| Висмут | 1.2 |
| Хромаль (Сплав 4,5 - 6% алюминия, 17 - 30% хрома, железа) | 1,3. 1,5 |
Сопротивление проводника определяется по формуле r = (ρ × l) / S, где:
- r - сопротивление проводника, Ом.
- ρ - удельное сопротивление проводника, Ом.
- l - длина проводника, м.
- S - сечение проводника, мм².
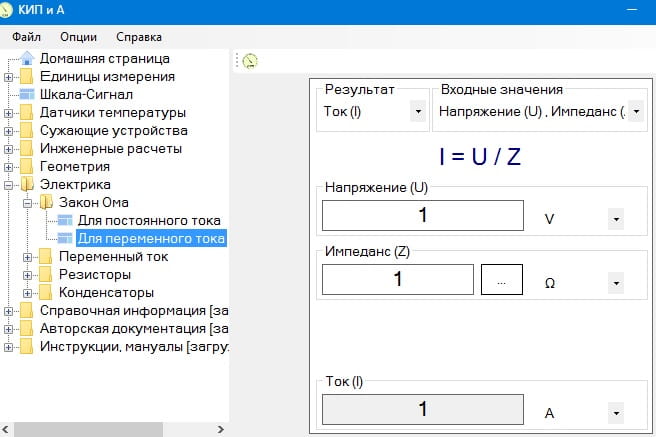
Закон Ома - скачать программу
Расчеты с использованием закона Ома также можно проводить в офлайн режиме. Для этого необходимо воспользоваться бесплатной программой «КИП и А». В пункте Электрика находится калькулятор, производящий расчеты по закону Ома для цепей постоянного и переменного тока: