Параметры лестницы, расчет оптимальной конструкции


При проектировании и строительстве лестницы важно добиться обеспечения безопасного передвижения заданной интенсивности и максимального удобства для человека. Помимо этого, стоит стремиться к минимизации пространства, занимаемого лестницей, путем выбора оптимального типа конструкции.
В процессе проектирования параметры лестницы должны вычисляться в зависимости от рассмотренных выше критериев и соответствовать нормативам. Допускается незначительная корректировка параметров, при условии сохранения безопасных и комфортных условий эксплуатации.
Параметры ступеней лестницы
Для определения параметров ступеней используется среднее значение человеческого шага при передвижении по горизонтальной поверхности. Данное значение варьирует в пределе от 60 до 64 см (среднее значение 62 см).
При расчетах значение шага по горизонтальной поверхности переноситься на шаг по лестнице. Исходя из этого, выделяют зависимость:
2m + sz = 62 (см), где m — высота ступени (подступенок) в см, sz — ширина ступени (проступь) в см.
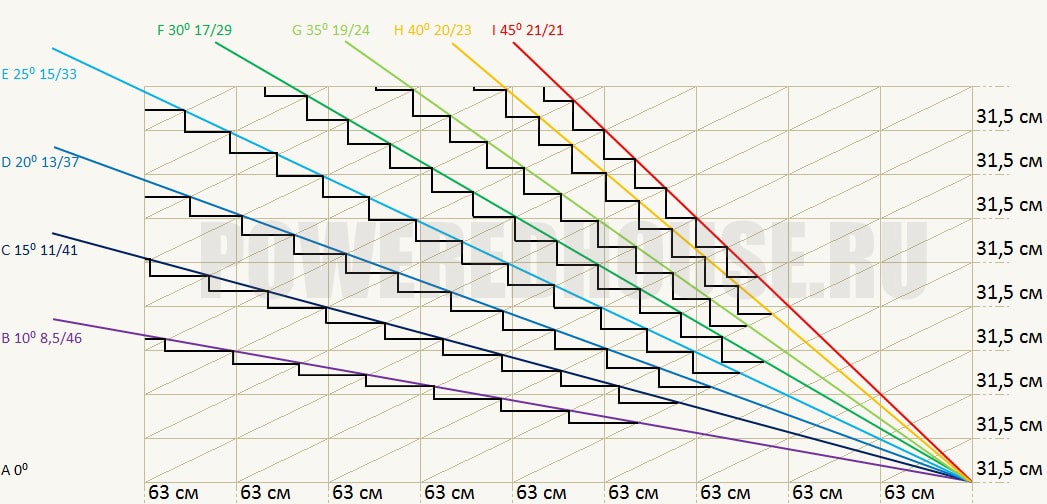
Таблица. Зависимость параметров лестницы от ее расположения.
При проектировании параметры лестницы указываются в виде дроби или умножения (15 / 33 или 15 × 33). В данных обозначениях 15 (см) — высота ступени (подступенка), 33 — ширина ступени (проступь).
Исходя из вышеописанной формулы, таблицы зависимости и зная одну из величин, можно с легкостью вычислить неизвестную величину.
Рассмотрим пример:
- Известно, что расстояние между уровнями лестницы (h) равно 2,5 метра.
- Следующие параметры, которые можно знать — угол наклона лестницы или длина проекции наклонной.
Необходимо определить параметры ступеней лестницы.
Решение:
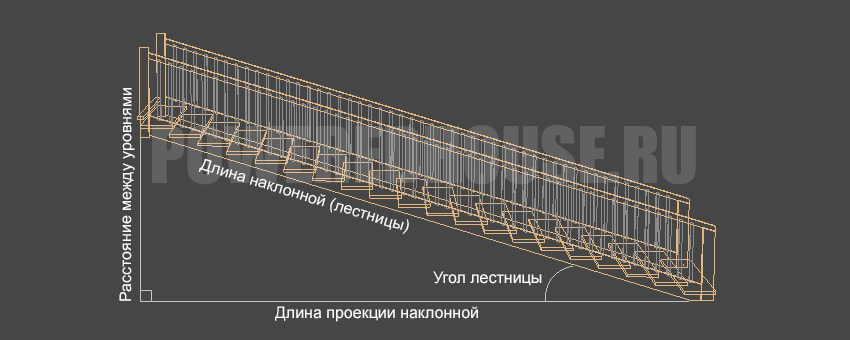
Допустим, известна длина проекции наклонной (l) — 4 метра. В первую очередь, нужно узнать длину наклонной (b) и угол наклона (α).
b — не что иное, как гипотенуза в треугольнике с катетами 2,5 и 4. Соответственно b = √(2,5² + 4²) = 4,72.
При известных сторонах треугольника углы проще всего определить, пользуясь теоремой косинусов. Соответственно, h² = l² + b² — 2 × l × b × cosα, откуда α = arccos((l² + b² — h²) / (2 × l × b)) × 180 / π. α ≈ 32°.
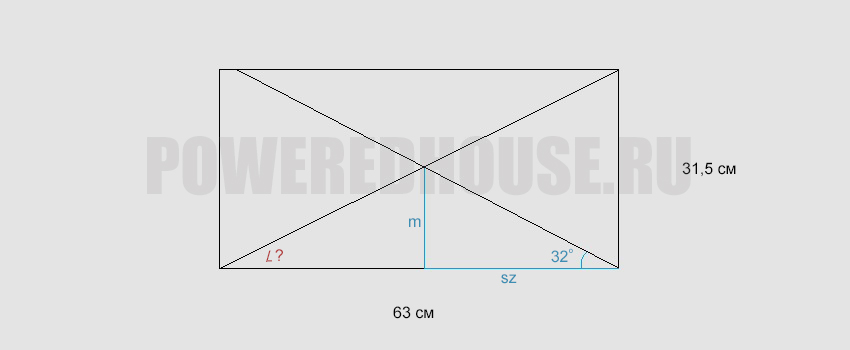
Теперь, исходя из таблицы зависимости параметров лестницы (изменения в соотношении размеров ступени в зависимости от угла подъема) и зная угол наклона, можно определить оптимальную высоту и ширину ступеней. Для наглядности рассмотрим увеличенный фрагмент зависимости:
В прямоугольном треугольнике с катетами 63 и 31,5 определим неизвестную гипотенузу и угол противолежащий катету со значением 31,5. Гипотенуза равна корню из суммы квадратов катетов. Рассчитав, получается значение 70,44. Теперь, зная три стороны треугольника, можно найти неизвестный угол по рассмотренной выше формуле. Получаем, угол = arccos((63² + 70,44² — 31,5²) / (2 × 63 × 70,44)) × 180 / π. Угол ≈ 26,56°.
Далее рассмотрим треугольник с углами 26,56°; 32°; 121,44° (180 — 32 — 26,56) и одной известной стороной, равной 63. Необходимо определить сторону, противолежащую углу 26,56°. Используем формулу для определения неизвестной стороны треугольника через известную сторону и два угла (написать формулу). Получаем, неизвестная сторона = (63 × sin(26,56 × (π / 180))) / sin(121,44 × (π / 180)) ≈ 33.
Рассчитанная сторона с размером 33 также является гипотенузой в треугольнике с катетами m и sz. По аналогии с предыдущим расчетом определим значение катета m (высота ступени). m = (33 × sin(32 × (π / 180))) / sin(90 × (π / 180)) ≈ 17,5. По теореме Пифагора sz (ширина ступени) = √(33² — 17,5²) ≈ 28.
Ответ: параметры (высота/ширина) ступеней лестницы с уклоном 32° — 17,5/28. Для сравнения, параметры лестницы с уклоном в 30° из таблицы зависимостей — 17/29.
Высоту и ширину ступеней нужно рассчитывать с точностью до миллиметра. Незначительное расхождение в размерах может дать недопустимое отклонение всей конструкции.
Параметры лестничных пролетов
Лестничные пролеты состоят из ступеней. Длина пролета зависит от количества ступеней, а ширина — от длины ступеней.
Лестничный марш включает в себя:
 |
Верхняя фризовая ступень. Ее поверхность находится на одном уровне с уровнем верхнего перекрытия или площадки. |
| Основные ступени. | |
| Нижняя фризовая ступень. Ее поверхность находиться на один подступенок выше нижнего перекрытия или основания. |
Минимально допустимое количество ступеней в одном марше – 3. Одна нижняя фризовая ступень, одна основная и одна верхняя фризовая ступень. Меньшее количество допустимо лишь в собственной квартире.
Длина лестничного пролета — это расстояние между крайними точками выступов нижней и верхней фризовой ступени. Для дугообразных или криволинейных лестниц данный параметр определяется по средней линии ходовой полосы.
Ширина лестничных маршей – это полезная длина ступеней без учета ограждений, вмонтированных осветительных приборов и иных конструктивных решений. Выделяют следующие рекомендуемые параметры полезной ширины пролетов:
- В жилом многоквартирном (более 10) доме: без лифта – 1,4 м; с лифтом – 1,2 м; эвакуационная лестница – 0,9 м.
- В жилом доме: до 10-ти квартир – 1,2 м; до 6-ти квартир – 1,1 м; до 2-х квартир – 1,0 м; с 1 квартирой – 0,9 м.
- Внутриквартирная лестница: прямая – 0,8 м; винтовая – 0,8 – 1,0 м.
- Внутриквартирная лестница, ведущая в нежилое помещение – 0,7 м.
- Подвальная лестница: в многоквартирном доме – 1,0 м; в одноквартирном доме – 0,8 м.
- Чердачная лестница – 0,7 м.
- Лестница дачного дома: наружная – 0,8 м; внутренняя – 0,8 м; чердачная – 0,6 м.
- Эвакуационная лестница – не менее 0,8 м.
При проектировании лестничных маршей нужно придерживаться следующих ограничений:
- Недопустимо наличие дверей на лестничных маршах.
- В габариты маршей не должны внедряться различные технические средства (счетчики газа или света).
- Для эвакуации в чрезвычайных случаях необходимо использовать только прямолинейные лестничные марши.
Параметры лестничных площадок
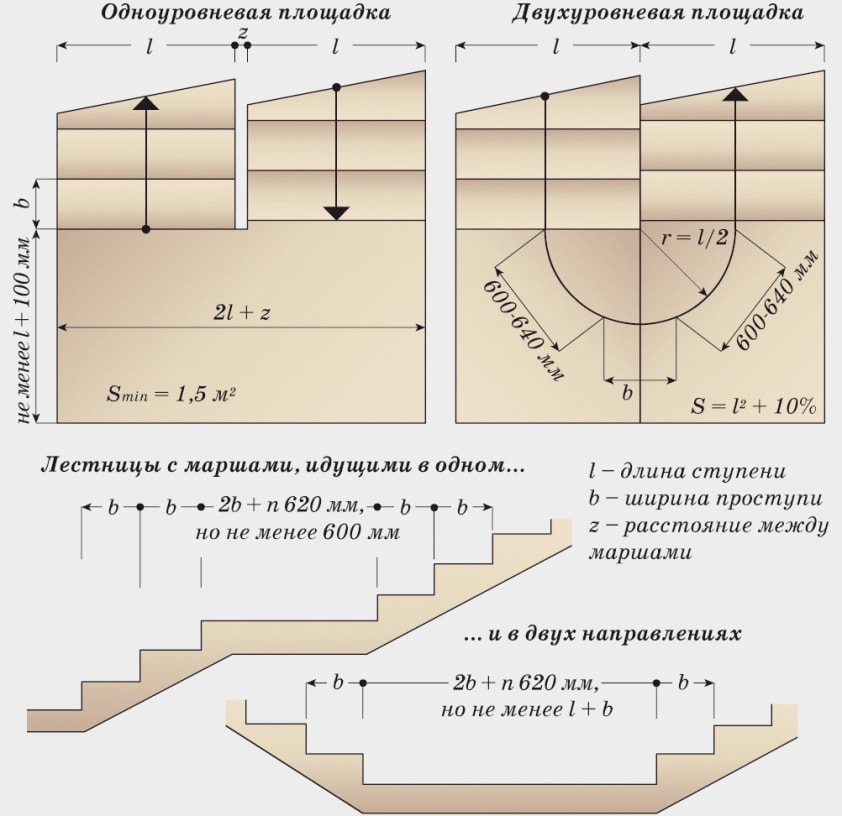
Лестничная площадка служит связующим звеном между маршами и обычно имеет прямоугольную форму. Конструкция лестницы в зависимости от конкретного проекта может иметь от одной до нескольких промежуточных площадок. Возможно и полное отсутствие площадок.
Длина лестничной площадки при расположении между двумя последовательными маршами должна составлять не менее 62 — 64 см (длина шага). Если лестничные марши расположены друг к другу под углом 135 — 180°, размер промежуточной лестничной площадки может и не равняться 64 сантиметрам. Соблюдать размер, равный длине шага, необходимо только в тех случаях, когда площадка лучеобразно делиться на две части или на две части параллельно движению марша и состоит из двух уровней.
Промежуточные лестничные площадки в жилых домах делаются обычно через каждые 10 — 14 ступеней, а в жилых помещениях — через 15 — 20 ступеней.
Согласно нормам, ширина лестничной площадки не должна быть меньше ширины марша.
Параметры ограждений, барьеров и поручней лестницы
Ограждение лестницы – защитная конструкция высотой не менее 1 метра с отверстиями, ширина которых не превышает 12 сантиметров. Ограждения (барьеры, решетки) обязательны для:
- Пандусов длиной более одного метра.
- Лестниц длиной более трех ступеней.
- Лестничных площадок (и иных конструкций, граничащих с открытым пространством) глубиной более 0,8 метров.
В случаях, когда ширина лестничного пролета превышает 3 метра, ограждения устанавливаются на обеих сторонах марша.
При анализе конструкций барьеров и ограждений используется параметр высоты пикирования, который определяется как разностью по высоте между высшей точкой ограждения и низшей точкой предыдущего, находящегося под ним уровня.
Таблица. Высота ограждений и барьеров в зависимости от угла подъема (спуска) лестницы и от высоты пикирования.
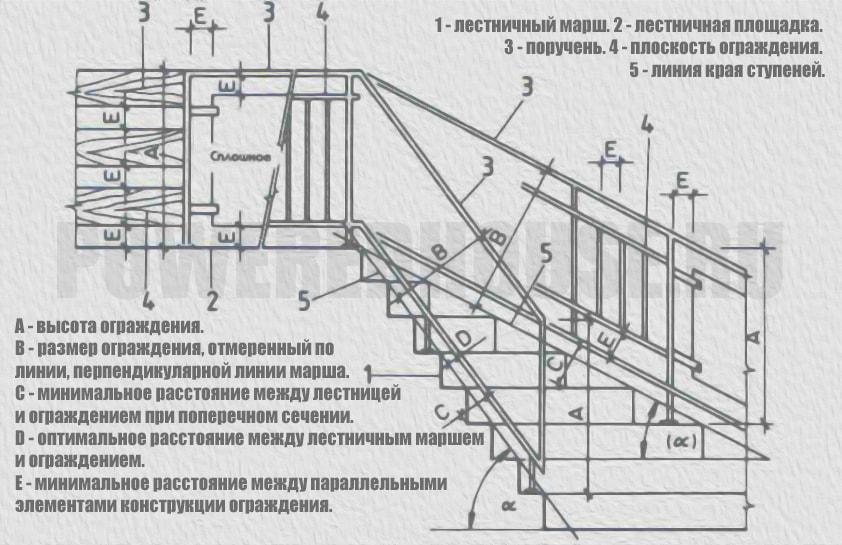 |
||||||
| Высота пикирования, м | Угол наклона уровней и маршей | А | В | С | D | Е |
| Минимальный размер, см | Максимальный размер, см | |||||
| 1 | 0 — 24 | 85 | 85 | Количество элементов | ||
| 24 — 60 | 42 — 85 | |||||
| 1 — 3 | 0 | 90 | 90 | 15 | ||
| 0 — 30 | 78 | 20 | 6 | |||
| 30 — 45 | 64 | 20 | 8 | |||
| 45 — 60 | 45 | 20 | 10 | |||
| 3 — 6 | 0 | 100 | 100 | 12 | ||
| 0 — 24 | 90 | 18 | 5 | |||
| 24 — 30 | 87 | 18 | 4 | |||
| 30 — 37,5 | 79 | 18 | 3 | |||
| 37,5 — 45 | 71 | 18 | 4 | |||
| 45 — 60 | 50 (60) | 18 | 8 | |||
| 6 — 12 | 0 | 110 | 110 | |||
| 0 — 24 | 100 | 18 | 5 | |||
| 24 — 30 | 96 | 18 | 4 | |||
| 30 — 37,5 | 87 | 18 | 3 | |||
| 37,5 — 45 | 78 (80) | 18 | 4 | |||
| 12 и выше | 0 | 120 | 120 | |||
| 0 — 24 | 110 | 18 | 5 | |||
| 24 — 30 | 105 | 18 | 4 | |||
| 30 — 37,5 | 95 | 18 | 3 | |||
Параметры свободного пространства между этажами (габарит)
Габарит лестницы — это свободное пространство, расположенное вверх по вертикали от воображаемой линии, соединяющей выступающие края ступеней.
Схема. Минимальный габарит при соединении лестничного марша с лестничной площадкой.
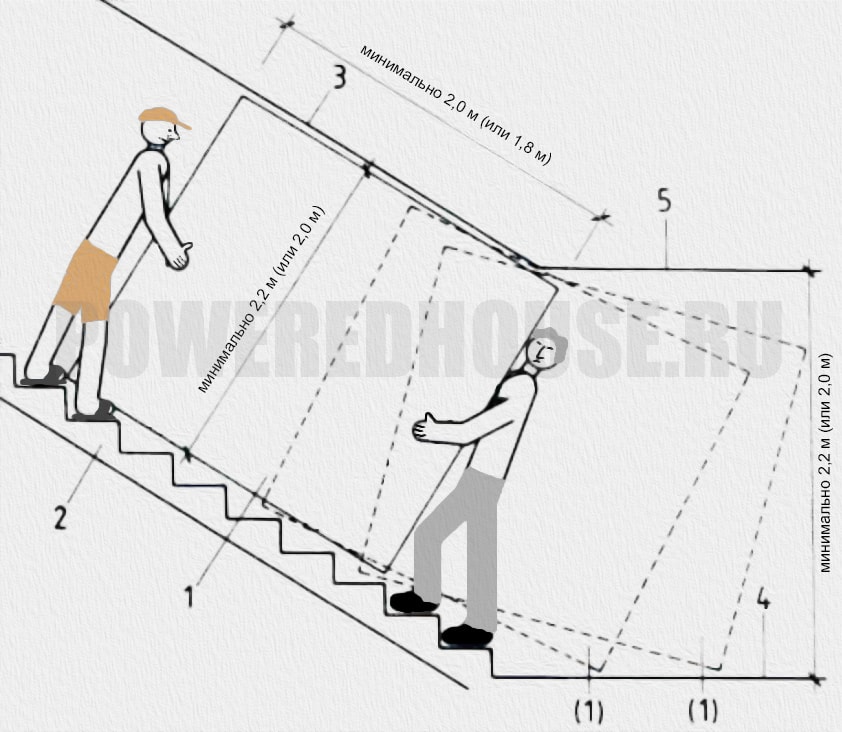 |
| 1 — передвигаемый предмет (груз) размером 200×180×60 см. |
| 2 — лестничный марш. |
| 3 — наклонное перекрытие следующего лестничного марша. |
| 4 — лестничная площадка. |
| 5 — верхнее перекрытие. |
Высота габарита должна позволять свободно перемещать по лестнице предметов длиной 2 метра и высотой 1,8 метра.
Для соблюдения требования по габариту высота над маршем и лестничной площадкой должна быть не менее 2,2 метра. Внутри квартиры, частного дома, а также применительно к лестницам, ведущим в подсобные помещения, высота над маршем может равняться 2,0 метрам.
Рассмотрев все необходимые параметры лестницы, в заключение можно выделить, что для получения удобной конструкции необходимо правильно подобрать угол спуска (подъема), оптимальную ширину марша, удобное ограждение и соответствующий нормам габарит.