Момент силы - онлайн калькулятор. Как найти и в чем измеряется момент силы, формулы

Момент силы - это векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение. По другому можно сказать, что момент силы – это произведение силы на плечо этой силы.
В данном обзоре приведен онлайн калькулятор момента силы, теоретические основы и формулы расчета момента силы.
Калькулятор момента силы
Для расчета момента силы (M) необходимо ввести в калькуляторе значения силы (F) и радиус-вектор (r). Также имеется возможность определять силу по известному моменту силы и радиус-вектору, и соответственно радиус-вектор по известной силе и моменту силы. Определившись с неизвестной величиной, введя известные значения и нажав кнопку «Вычислить», вы получите нужный результат.
Момент силы - определения и формулы
При вращательном движении линейные кинематические характеристики (пройденный путь s, линейная скорость υ, тангенциальное ускорение aτ) пропорциональны соответствующим угловым характеристикам. При этом коэффициентом пропорциональности является радиус вращения r. В качестве силовой характеристики вращательного движения вводится понятие момента силы. Следует отличать моменты силы относительно оси и относительно точки.
Момент силы относительно точки O
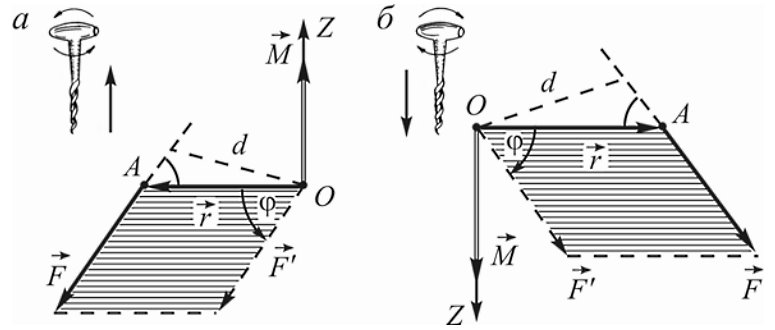
Моментом силы относительно точки O называется векторное произведение M→ = [r→, F→], где r→ - радиус-вектор, проведенный из этой точки к точке приложения силы. Вектор M→ перпендикулярен плоскости, в которой лежат векторы r→ и F→, и численно равен площади параллелограмма, сторонами которого являются данные векторы M = rFsinφ.
 |
|
| Направление вектора M→ определяется по правилу векторного произведения: если совместить точки приложения векторов r→ и F→, то кратчайший поворот от радиус-вектора r→ к силе F→′ будет происходить против часовой стрелки, если смотреть с вершины вектора M→. |
Иногда удобнее смотреть вслед вектору M→, тогда кратчайший поворот от радиус-вектора r→ к силе F→′ будет происходить по часовой стрелке. На практике удобно определять направление вектора M→ по правилу правого винта: если вращать головку винта в направлении действия силы, то его поступательное движение покажет направление момента силы M→. |
Момент силы равен нулю, если равна нулю сила или линия действия силы проходит через точку O.
 |
|
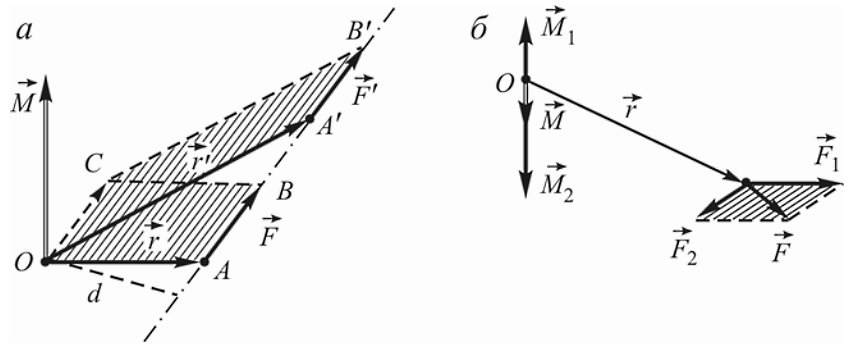
| Момент силы M→ не изменяется, если вектор F→ (точку приложения силы) переносить вдоль линии действия. Наглядно видно, что площади параллелограммов OABC и OA′B′C равны, поскольку они имеют общее основание OC и высоту d. | Геометрическая сумма моментов нескольких сил, действующих на материальную точку A относительно некоторой точки O, равна моменту суммы этих сил относительно той же точки M→ = [r→, F→] = [r→,(F→1+F→2 +...)] = [r→,F→1]+[r→,F→2]+... |
Момент силы относительно некоторой оси
Моментом силы относительно некоторой оси называют проекцию Mz на данную ось вектора момента этой силы M→ относительно любой точки, лежащей на оси.
Величина Mz не зависит от выбора точки O‘ на оси, поскольку момент силы M при переносе точки приложения силы вдоль линии ее действия не изменяется. Момент силы относительно точки O численно равен моменту этой силы относительно оси OZ, перпендикулярной плоскости, в которой лежат векторы r→ и F→ (а значит и точка O).
Плечо силы - это кратчайшее расстояние между осью и линией действия силы d = r sinφ. В таком случае момент силы относительно этой оси может быть определен как произведение силы и плеча M = Fd. Такое определение момента силы дается в элементарной физике. При этом положительными считаются те моменты сил, которые вызывают вращение по часовой стрелке, а отрицательными - вызывающие вращение против часовой стрелки.
Рассмотрим действие сил на тело, способное вращаться вокруг неподвижной оси OO′:
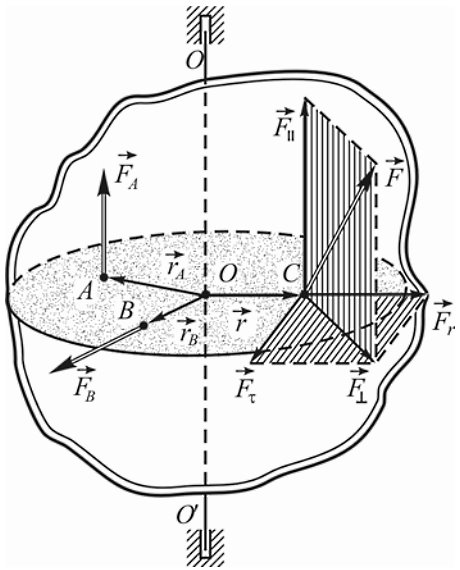
Сила F→a, параллельная оси, может только деформировать эту ось. Не вызовет вращения и сила F→b, лежащая в плоскости, перпендикулярной оси вращения, если линия, вдоль которой она действует, проходит через эту ось, то есть совпадает по направлению с радиус-вектором r→b, проведенным в точку ее приложения B.
Вызвать вращение тела вокруг неподвижной оси может только сила или ее составляющая, которая лежит в плоскости, перпендикулярной данной оси, и не совпадает по направлению с радиус-вектором, проведенным в этой плоскости к точке ее приложения. Силу, образующую произвольный угол с осью вращения, можно спроецировать на перпендикулярную плоскость, а затем разложить на тангенциальную F→τ и радиальную F→r составляющие. Именно тангенциальная составляющая силы создает момент относительно оси M = F→τr и является причиной тангенциального ускорения точки тела, к которой она приложена, то есть вызывает изменение модуля линейной скорости этой точки при вращательном движении.








