Комплексные числа — простое объяснение. Сложение, вычитание, умножение и деление комплексных чисел

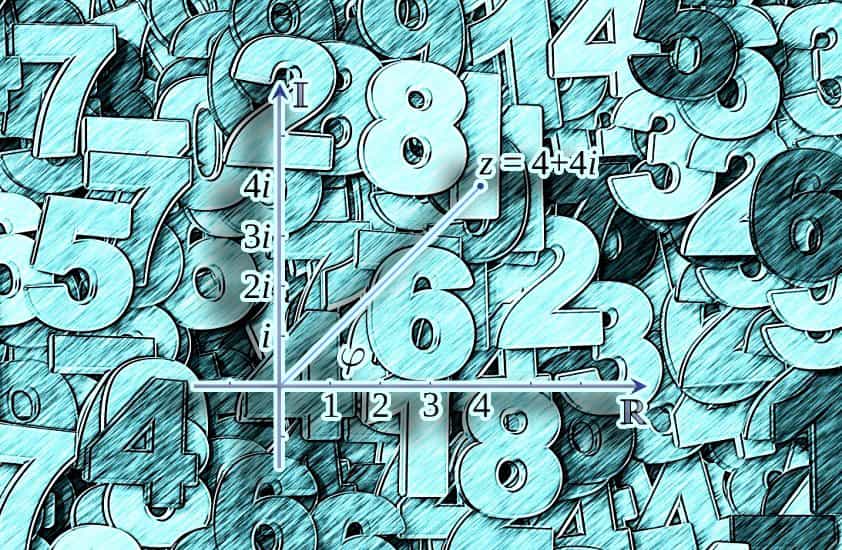
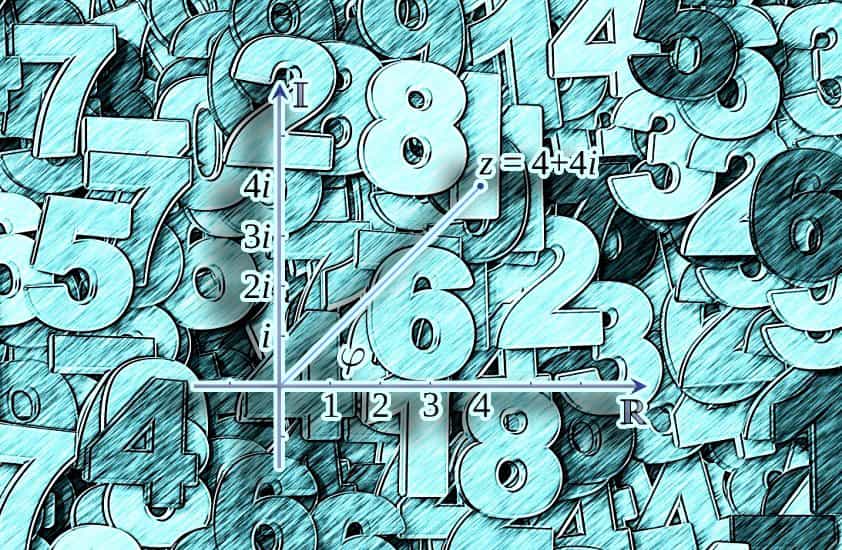
Комплексные числа — простое объяснение

Для того, чтобы разобраться с комплексными числами, следует для начала рассмотреть множество действительных чисел. К этому множеству относятся целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.

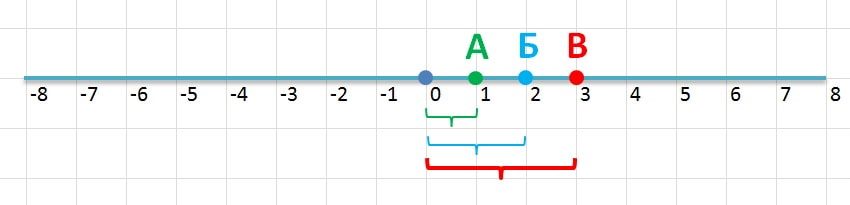
Рассмотрим две точки на прямой А = 1 и Б = 2. Сложим эти две точки. Их сумма эта третья точка В = 1+2 = 3.

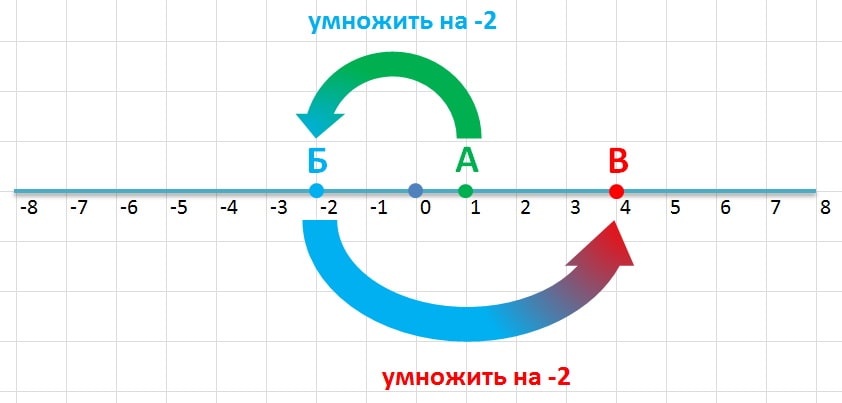
Точки также можно перемножать. Посмотрим, например, как действует умножения на минус 2. Данное действие преобразует точку 1 в минус 2.  Если мы снова умножим на минус 2, то нужно будет повторить аналогичное передвижение на прямой, поменять стороны относительно начала координат и удвоить расстояние до него. В результате получим 4.

Умножение на минус 1 устроено просто. Каждая точка переходит в симметричную ей относительно начала координат. Другими словами нужно сделать пол оборота (повернуть на 180°). Повторение умножения на минус 1 приводит в исходное положение. Умножение на минус 1 переводит 1 в минус 1. Если еще раз умножить на минус 1, мы вернемся обратно в 1.

На данном этапе можно выделить правило, что если умножить число на себя, результат всегда будет положительным. Другими словами минус 1 не имеет квадратного корня. Но только не в случае с комплексными числами.

В начале 19 века Робер Арган высказал следующую идею. Поскольку умножить на минус 1 означает повернуть на 180°, то квадратный корень из минус 1 означает повернуть на половину (90°). Если повернуть дважды на четверть оборота, вы сделаете пол оборота. Квадрат четверти оборота — это пол оборота (минус 1). То есть квадратный корень из минус 1 отвечает точке, в которую минус 1 переходит при повороте на 90°. Поскольку такое построение, выходящее за пределы горизонтальной прямой, выглядит странным, говорят, что такая точка, являющаяся квадратным корнем из минус 1 — это мнимое число. И в математике оно обозначается — i.

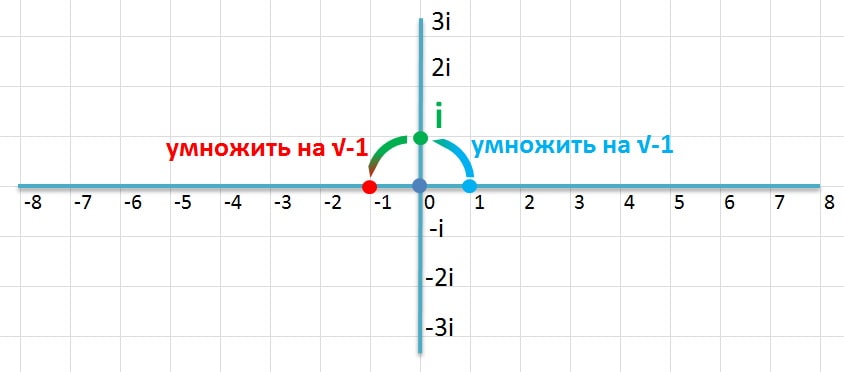
С выходом за пределы прямой, все последующие действия производятся легко. Можно отметить числа 2i, 3i и так далее. Каждой точке плоскости отвечает комплексное число. И наоборот — всякое комплексное число задает точку на плоскости.

Операции с комплексными числами

Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания, умножения и деления. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел. Например, нельзя указать, какое из двух комплексных чисел больше или меньше.

Сложение и вычитание комплексных чисел

Комплексные числа могут складываться и вычитаться как обычные.

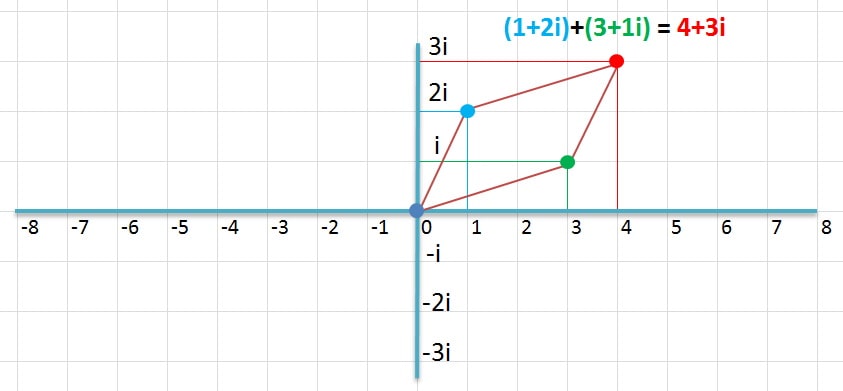
Рассмотрим точку, обозначающую число 1+2i. Прибавим к нему число 3+1i. Можно сложить столбиком и получить 4+3i. Геометрически это обычное сложение векторов.

Разность комплексных чисел, записанных в алгебраической форме, представляет собой комплексное число, действительная часть которого и коэффициент при мнимой части равны соответственно разности действительных частей и разности коэффициентов при мнимой части уменьшаемого и вычитаемого.

В общем виде вычитание комплексных чисел z1 = a+bi и z2 = c+di можно записать так: z1-z2 = (a+bi)-(c+di) = (a-c)+(b-d)i.

Несколько примеров вычитания:

• (5+9i)-(3+24i) = (5-3)+(9-24)i = 2-15i.
• (-4+16i)-(11-8i) = (-4-11)+(16+8)i = -15+24i.

Умножение и деление комплексных чисел

Комплексные числа перемежаются точно также, как и действительные числа. Рассмотрим несколько примеров.

2×(1+1i) = 2+2i. Геометрически умножение на два выглядит как растягивание прямой с точкой на плоскости в два раза.

Умножать на i также не сложно. Известно, что i отвечает четверти оборота. Например, чтобы умножить 3+1i на i, достаточно повернуть точку на четверть оборота. Получаем -1+3i.

Умножим два комплексных числа 2+1,5i и -1+2,4i:

Сначала нужно умножить (-1+2,4 i) на два, затем на 1,5i. Далее складываются результаты. (2+1,5i)×(-1+2,4i) = 2(-1+2,4i)+1,5i(-1+2,4i) = -2+4,8i-1,5i+3,6×i×i. i в квадрате равно минус 1. Соответственно -2+4,8i-1,5i+3,6×i×i = -2+4,8i-1,5i-3,6 = -5,6+3,3i.

Частное комплексных чисел z1 = x1+y1i и z2 = x2+y2i в алгебраической форме находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:

z1÷z2 = (x1+y1i)÷(x2+y2i) = ((x1+y1i)×(x2-y2i))÷((x2+y2i)×(x2-y2i)) = ((x1×x2+y1×y2)÷(x2²+y2²)) + (i×(x2×y1-x1×y2)÷(x2²+y2²)).

Рассмотрим пример деления -1+3i на 1+2i. Используя формулу для нахождения частного, получаем:

z1÷z2 = (-1+3i)÷(1+2i) = ((-1+3i)×(1-2i))÷((1+2i)×(1-2i)) = ((-1×1+3×2)÷(1²+2²))+(i×(3×1+(-1)×(-2))÷(1²+2²)) = 5÷5+i×5÷5 = 1+i.

Комплексные числа — тригонометрическая форма

Казалось бы, плоскость двухмерная, так как для описания произвольной точки нужны два числа. На самом же деле можно обойтись одним числом. Для этого используется тригонометрическая форма представления. То есть z = a+bi можно представить как z = [z]×(cosφ+i×sinφ), где:

• [z] — модуль комплексного числа. Это расстояние от соответствующей точки до начала координат на плоскости. Например, модуль 2 + 1,5i = 2,5.
• φ (argz) — аргумент комплексного числа. Он находится измерением угла между осью абсцисс и прямой, соединяющей начало координат с точкой, отвечающей числу. Аргумент 2 + 1,5i = 36,8°.

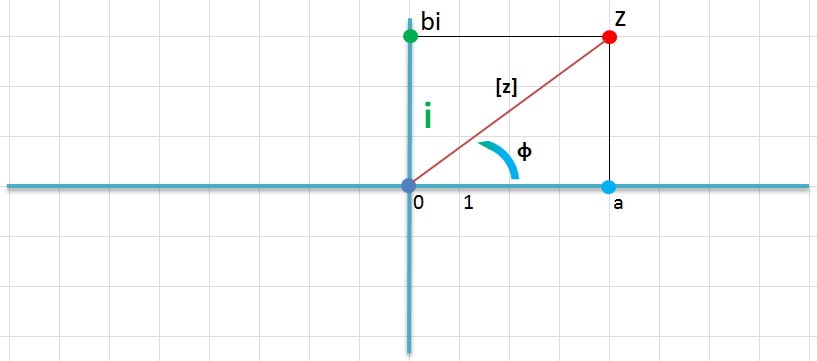
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: [z] = √(a²+b²). Данная формула справедлива для любых значений a и b.

Для нахождения аргумента (φ или argz) нужно воспользоваться следующими формулами:

• Если a>0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле argz = arctg(b/a).
• Если a<0, b>0 (2-я координатная четверть), то аргумент нужно находить по формуле argz = π+arctg(b/a).
• Если a<0, b<0 (3-я координатная четверть), то аргумент нужно находить по формуле argz = -π+arctg(b/a).