Генератор переменного тока и синусоида — самое простое объяснение

Устройство, позволяющее получить переменный ток, называется генератором переменного тока. Задача генератора переменного тока создать изменяющиеся со временем ЭДС или напряжение.
Принцип работы генератора переменного тока
Чтобы понять принцип работы генератора переменного тока необходимо изучить поведение системы под действием ЭДС или напряжения в зависимости от времени по закону гармонических колебаний (ξ(t) = ξmax×cosωt; U(t) = Umax×cosωt). Создавая в колебательной системе переменную ЭДС (или подавая напряжение) мы получим ток I(t), который протекает в этой системе. Ток тоже будет меняться по гармоническому закону I(t) = Imax×cos(ωt+φ), и он будет переменным.
В основе практически всех генераторов тока лежит проводящая рамка, вращающаяся в магнитном поле. В этой рамке может быть много витков. Для общего понимания можно рассмотреть рамку, состоящую из одного витка.
В примере магнитное поле создается постоянным магнитом. Рамка находится между полюсами, подключена к внешней цепи и вращается вокруг своей оси. Линии магнитного поля выходят из северного полюса и входят в южный полюс магнита (направление вектора магнитной индукции (B) на схеме сверху вниз). Нормаль к рамке (n) в данный момент тоже направлена сверху вниз.
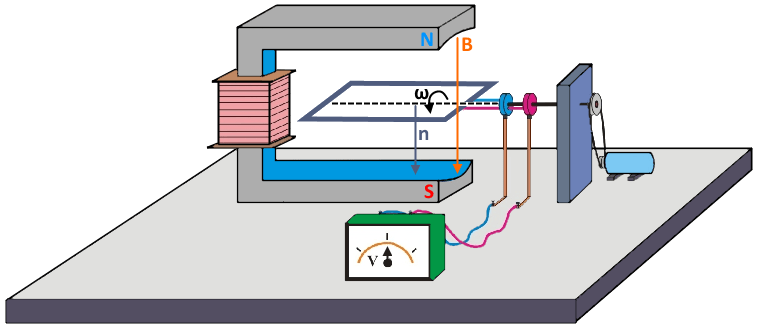
Подсоединим эту рамку к цепи через кольцевые контакты и щетки. Рамка — это контур, находящийся в магнитном поле. Через этот контур магнитным полем создается магнитный поток Φ = B×S×cosα (B — модуль вектора магнитной индукции; S — площадь рамки; α — угол между направлением нормали и направлением магнитного поля). Если рамка вращается с угловой скоростью ω, то угол α меняется с течением времени α = ω×t+φ0. φ0 — это начальный угол между нормалью к рамке и вектором магнитной индукции. С учетом приведенной схемы (рамка расположена так, что ее плоскость перпендикулярна магнитному полю) φ0 = 0. Если α меняется с течением времени, то и магнитный поток будет меняться с течением времени Φ(t) = B×S×cos(ω×t+φ0). Если в рамке меняется магнитный поток, то в ней по закону Фарадея возникает электродвижущая сила электромагнитной индукции ξi = -Φ’ (Φ’ — производная по времени магнитного потока). Получаем следующую формулу ξi(t) = -(B×S×cos(ω×t+φ0))’ = +B×S×sin(ω×t+φ0)×ω.
Пусть φ0 = π/2, тогда sin(α+π/2) = cosα. Соответственно ξi(t) = B×S×ω×cos(ω×t) или ξi(t) = ξmax×cos(ω×t) (ξmax = B×S×ω). Эта формула относится к рамке, состоящей из одного витка. Для рамки из N последовательно соединенных витков ξi(t) = ξmax×cos(ω×t) (ξmax = N×B×S×ω).
В идеальном генераторе (внутреннее сопротивление обмотки равно 0 Ом) напряжение на выходе будет совпадать с ЭДС. U(t) = Umax×cos(ω×t) (Umax = N×B×S×ω).
На выходе генератора напряжение (ЭДС) меняется по гармоническому закону. Циклическая частота напряжения (ЭДС) равна угловой скорости вращения рамки. Амплитуда напряжения (ЭДС) на выходе генератора прямо пропорциональна числу витков в рамке, площади рамки, величине магнитного поля, частоте вращения рамки.
Рассмотренная модель позволяет понять принцип работы генератора переменного тока. В реальных генераторах, как правило, вращается не рамка, а магнит вокруг рамки. Также вместо постоянного магнита используется электромагнит. Вращающийся электромагнит называется ротором, а неподвижная часть с рамкой — статором.
Проводник в магнитном поле — сила Лоренца
Рассмотрев теоретические основы работы генератора переменного тока перейдем к более детальному объяснению. Для этого разберемся с проводником, передвигающимся в магнитном поле. Ведь, по сути, рамку можно представить как систему проводников, а вращение — как движение.
Если передвигать проводник в магнитном поле таким образом, чтобы он пересекал силовые линии поля, то в проводнике будет индуктироваться ЭДС. Для определения направления индуктированной ЭДС в проводнике служит правило правой руки.
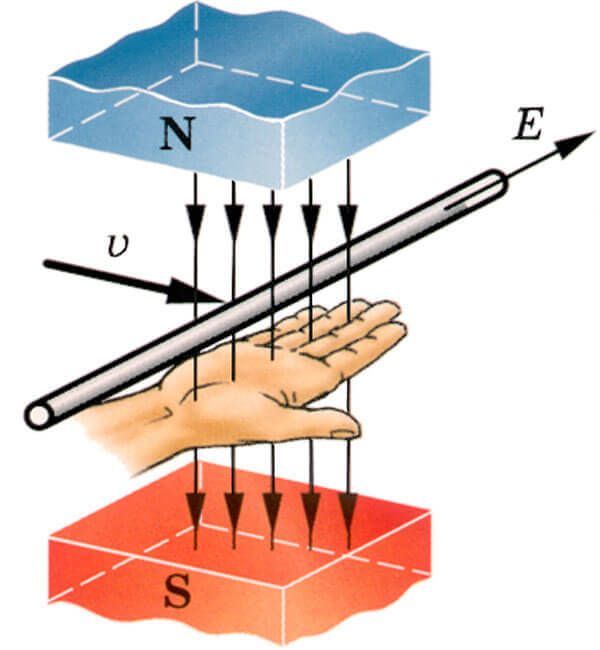
Если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут указывать направление индуктированной ЭДС в проводнике.
Если проводник замкнуть на какую-либо нагрузку, то в нем возникнет ток. Ток создаст свой магнитный поток. Взаимодействие тока и магнитного поля полюсов создаст тормозящую силу (сила Лоренца), действующую на проводник в направлении противоположном его движению.
Сила Лоренца – это сила, которая действует на электрически заряженную частицу при ее движении в магнитном поле. Ее направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Для определения направления силы Лоренца можно пользоваться правилом левой руки.
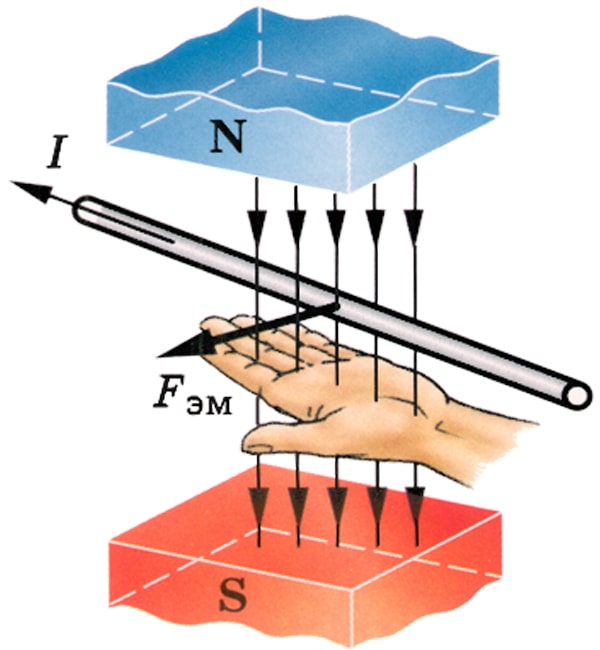
Если левую руку расположить так, чтобы линии магнитного поля входили в ладонь перпендикулярно ей, а четыре пальца были направлены по движению положительно заряженной частицы (или против движения отрицательно заряженной частицы), то отставленный большой палец покажет направление действующей на проводник силы. Если заряд отрицателен, то направление силы нужно сменить на противоположное.
Рассмотрим пример, в котором цилиндрический проводник движется в постоянном магнитном поле. Его вектор скорости υ→ перпендикулярен оси цилиндра, а вектор индукции магнитного поля B→ перпендикулярен, как оси проводника, так и его скорости.
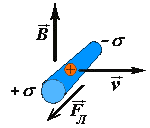
Вместе проводником движутся и свободные заряды, находящиеся внутри него. Со стороны магнитного поля на эти заряды будут действовать силы Лоренца, направленные вдоль оси проводника. В металлах свободными зарядами являются отрицательно заряженные частицы — электроны. Однако мы будем рассматривать движение положительно заряженных частиц, так как за направление тока принимают направление положительных частиц.
В неподвижном проводнике свободные заряды движутся хаотически равновероятно во все стороны, поэтому среднее значение вектора силы Лоренца равно нулю. При движении проводника на хаотическое тепловое движение свободных зарядов накладывается направленное движение проводника. Благодаря движению появляется отличная от нуля результирующая сила Лоренца, одинаковая для всех частиц проводника и приводящая к возникновению электрического тока.
Под действием силы Лоренца свободные заряды смещаются к торцам цилиндра. Такое перераспределение зарядов на концах проводника приводит к созданию электрического поля. Здесь важно отметить, что действие поля на заряженные частицы будет направлено в сторону противоположную силе Лоренца. Но при постоянной скорости движения проводника установится равновесие, при котором движение зарядов прекратится несмотря на наличие электрического поля. В таких условиях сила Лоренца FL=qυB, действующая на частицу, будет уравновешена силой со стороны электрического поля Fel=qE. Приравнивая эти силы, можно определить напряженность электрического поля в проводнике E=υB.
Так как сила Лоренца одинакова во всех точках проводника, то и электрическая сила также должна быть постоянна, то есть возникшее электрическое поле является однородным. Это электрическое поле можно также характеризовать разностью потенциалов между торцами цилиндра, которая равна Δφ=El=υBl, где l — длина проводника.
Сила Лоренца, действующая на свободные заряды в проводнике, может являться сторонней силой. Тем самым она будет приводить к возникновению электрического тока в замкнутом контуре, если к движущемуся проводнику подключить нагрузку.
Для создания замкнутой цепи с нагрузкой-резистором R дадим проводнику AC скользить по двум параллельным шинам (рельсам), соединенным между собой. Вся система помещена в однородное магнитное поле, вектор индукции которого B→ перпендикулярен плоскости шин. Для упрощения примем, что сопротивления шин и движущегося проводника (перемычки) пренебрежимо малы по сравнению с сопротивлением соединяющего резистора R. Если к подвижному проводнику приложить внешнюю силу F→, то он придет в движение.
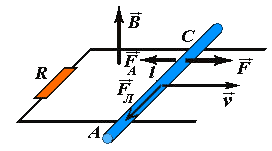
Под действие силы Лоренца свободные заряды в проводнике придут в движение, создавая избыточные заряды на концах. Эти заряды создадут электрическое поле во всем контуре, образованном перемычкой, шинами и соединяющим резистором, поэтому в контуре возникнет электрический ток. Сила Лоренца, действующая на заряды движущегося проводника, будет играть роль сторонней, преодолевающей силы, действующие со стороны электрического поля. Работа этой силы (ЭДС) по перемещению единичного заряда равна произведению силы Лоренца на расстояние между шинами ε = (1/q)FLl=υBl.
Несмотря на то, что это выражение для ЭДС полностью совпадает с формулой (Δφ=El=υBl) для разности потенциалов, ее смысл принципиально иной. Разность потенциалов — это возможная работа сил электрического поля. В рассматриваемой цепи направление движения заряженных частиц противоположно направлению силы со стороны электрического поля. То есть сила Лоренца совершает стороннюю работу против сил электрического поля, а электрическое поле совершает положительную работу, проталкивая заряженные частицы по шинам и соединяющему резистору (внешней цепи).
Работа генератора и синусоида переменного напряжения (ЭДС) — самое простое объяснение
Минимально вдаваясь в теоретические особенности работы генератора, вектора магнитной индукции, силу Лоренца, закон Фарадея, сложные для восприятия формулы, попробуем как можно проще все объяснить на простых примерах. После того как вы поймете все процессы генерации напряжения и тока на микроуровне, можно смело переходить к прочтению академической писанины с кучей умных слов и непонятных формул. У вас появится шанс что-то понять и осмыслить. И когда вы услышите фразу индуцированная ЭДС, вы будете четко понимать ее смысл, а не будете оперировать размытыми определениями.
Начнем с классической рамки, вращающейся в магнитном поле. В реальных генераторах как правило магнитное поле вращается вокруг рамки (обмоток), но от перемены мест слагаемых сумма не меняется, поэтому для простоты моделирования будем рассматривать именно вращение рамки.
Линии магнитного поля выходят из северного полюса и входят в южный полюс магнита. Мы не будем акцентировать внимание на конкретное направление линий магнитного поля, так как это для упрощенной модели объяснения не принципиально.
Изобразим схематически рамку в магнитном поле:
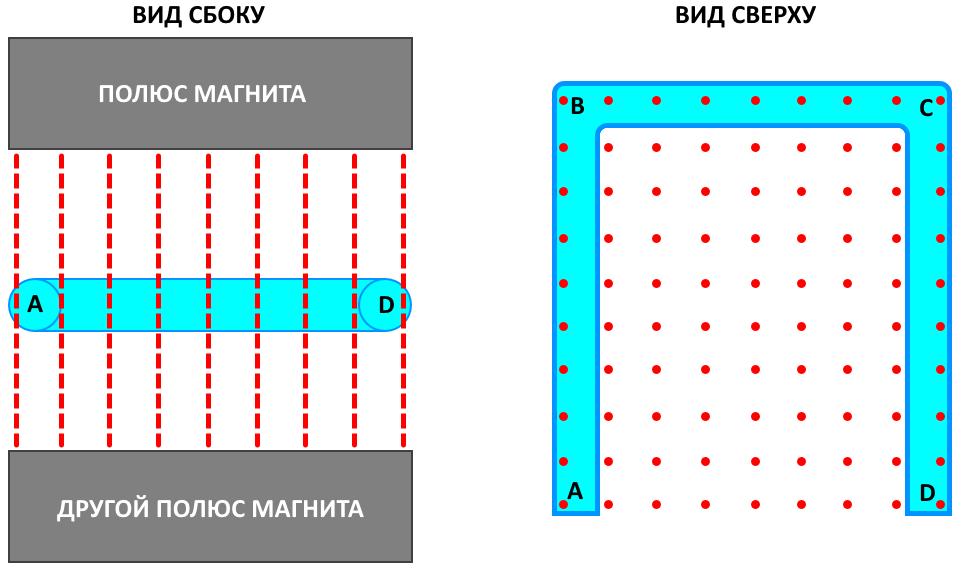
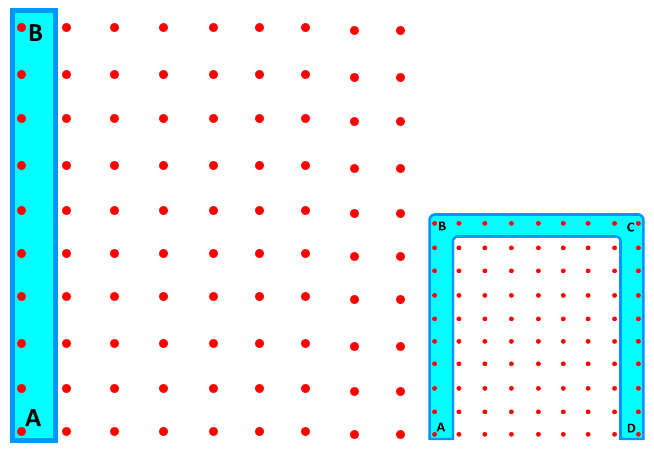
Несмотря на то, что в магнитное поле, условно показанном красными линиями, помещено нечто похожее на букву «П», это нечто и есть рамка из проводника. В электротехнике рамка — это проводник, согнутый в форме прямоугольника. Можно конечно было продлить проводник от точек A и D навстречу, но это опять-таки непринципиально пока цепь не замкнута.
Вернемся к рамке. По сути она состоит из трех отрезков проводника AB, BC и CD. При вращении рамки линии магнитного поля пересекают только участки AB и CD. То есть отрезок BC можно откинуть.
Известно, что если перемещать проводник в магнитном поле из стороны в сторону, то при движении в одну сторону свободные заряды (электроны) смещаются к одному концу проводника, при движении в другую сторону — к другому концу проводника. Вращение рамки — это тоже движение, при котором участок AB перемещается в одну сторону в то время, как участок CD перемещается в другую сторону:
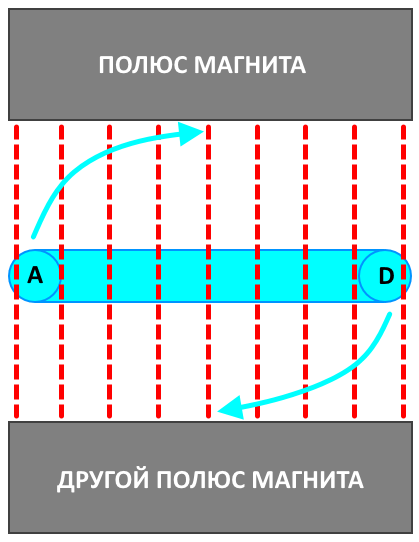
Так как у нас простое объяснение, то на данном этапе целесообразно перейти от рассмотрения вращающейся рамки к вращающемуся (движущемуся) проводнику в магнитном поле. Для этого оставим только участок АС. Для понимания отметим, что участок CD просто увеличивал ЭДС, а убрав его ЭДС цепи уменьшилась в два раза. Чтобы получить ту же ЭДС с одним проводником (в нашем случае участок AB), его длину следовало бы увеличить в два раза:
Теперь важно уточнить особенность вращения в разрезе движения проводника. Для этого приведем следующую модель:
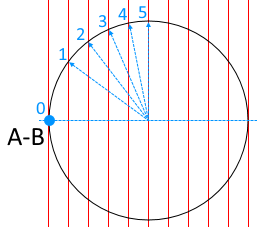
Проводник AB перемещается в магнитном поле по траектории окружности. Конец проводника A мы видим, а конец B находится за плоскостью чертежа. Двигаясь по окружности проводник с разной скоростью пересекает линии магнитного поля и это наглядно видно. Так путь от точки 0 до точки 1 больше пути от точки 1 до точки 2. И так далее вплоть до точки 5. От точки 5 и далее по траектории скорость пересечения линий магнитного поля уменьшается, потом, проводник уже движется в другую сторону, опять увеличивается и уменьшается до точки 0.
Что нам дает скорость пересечения проводника с линиями магнитного поля? Чем она больше, тем сильнее воздействие магнитного поле на свободные электроны в проводнике, и тем больше электронов переместятся к одному из концов проводника. Чем больше электронов скопиться у одного из концов проводника, тем большая будет разность потенциалов между точками A и B.
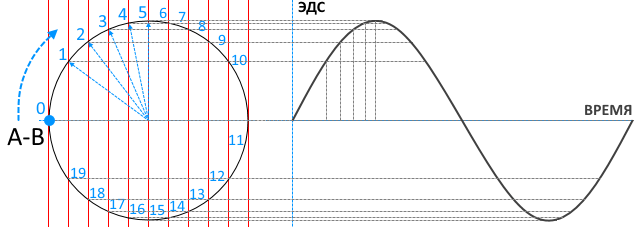
Сделаем проводником один оборот по окружности в магнитном поле и проанализируем разность потенциалов между его концами (синусоида):
 |
|
| Точка 0 | В данной точке изначально находится проводник. Заряды в проводнике движутся хаотически равновероятно во все стороны, но при этом они равномерно распределены по всей длине. Потенциал на конце A = 0 Вольт, на конце B = 0 Вольт. То есть разности потенциалов между концами проводника нет. |
| Точка 1 | Дойдя до точки 1 проводник пересечет определенное количество линий магнитного поля, что вызовет смещение определенного количества электронов к одному из концов проводника, например к концу A. Соответственно конец A будет заряжен отрицательно, а конец B — положительно. Образуется разность потенциалов (ЭДС), как показано схематически на графике (синусоида). Если проводник прекратит движение, то электроны вернутся на свои места и равномерно перераспределятся, пропадет разность потенциалов. Но проводник продолжает двигаться. |
| Точка 2 | Время потраченное на прохождение от точки 1 до точки 2 значительно меньше времени прохождения от точки 0 до точки 1. Соответственно двигаясь в этом секторе проводник намного быстрее будет пересекать линии магнитного поля. Электроны продолжат скапливаться у конца A, но делать они это будут намного интенсивнее. Также увеличится разность потенциалов (ЭДС) между концами A и B. |
| Точка 5 | Возле точки 5 проводник пересекает линии магнитного с максимальной скоростью. В точке 5 будет наибольшая разность потенциалов (ЭДС) между концами A и B. |
| Точка 11 | От точки 5 до точки 11 скорость пересечения проводником линий магнитного поля уже будет постепенно убывать. Электроны постепенно будут возвращаться в исходное положение и в точке 11 между концами A и B пропадет разность потенциалов. |
| Точка 15 | От точки 11 к точке 15 и далее к точке 0 проводник уже будет двигаться в другом направлении. Соответственно картина перераспределения зарядов будет аналогичной, только электроны уже будут накапливаться у конца B и затем возвращаться в исходное положение в точке 0. |
Один оборот проводника за секунду — это 1 Гц. Соответственно 50 Гц — это 50 оборотов в секунду, и за это время электроны 50 раз сконцентрируются у одного конца проводника и 50 раз — у другого конца проводника.
Мы разобрались, что при движении проводника (вращении рамки) в магнитном поле на концах проводника образуется переменная электродвижущая сила (разность потенциалов между концами A и B), которую графически можно представить синусоидой. Если подсоединить к концам проводника нагрузку (замкнуть цепь), то имеющаяся разность потенциалов создаст электрическое поле и во внешней цепи появится переменный ток.
Важно отметить следующую интересную особенность — при движении проводника (вращении рамки) в магнитном поле разность потенциалов создает электрическое поле не только во внешней (подключенной к проводнику) цепи, но и в самом проводнике. Но движение зарядов в проводнике происходит против силы электрического поля. Этому способствует сила Лоренца, совершающая стороннюю работу. Сила Лоренца не появится, если проводник не будет двигаться в магнитном поле. А чтобы проводник двигался, кто-то или что-то должно его двигать. В этом и заключается основная особенность работы генератора переменного тока.








